题目内容
4.如果二次函数的二次项系数为1,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此二次函数的特征数,如函数y=x2-x+3的特征数为[-1,3].若一个二次函数的特征数是[2,-1],则将此函数的图象先向左平移1个单位,再向下平移1个单位后,得到的图象对应的函数的特征数是(4,1).分析 根据特征数的定义写出抛物线解析式,然后整理成顶点式形式并求出顶点坐标,再根据向左平移横坐标减,向下平移纵坐标减求出平移后的抛物线顶点坐标,然后利用顶点式形式写出解析式,再整理成二次函数一般形式,然后写出特征数即可.
解答 解:∵二次函数的特征数是[2,-1],
∴二次函数解析式为y=x2+2x-1=(x+1)2-2,
∴函数顶点坐标为(-1,-2),
∵向左平移1个单位,向下平移1个单位,
∴平移后的函数图象顶点坐标为(-2,-3),
∴函数解析式为y=(x+2)2-3=x2+4x+1,
即y=x2+4x+1,
所以,特征数是(4,1).
故答案为:(4,1).
点评 本题考查了二次函数图象与几何变换,平移的规律:左加右减,上加下减,利用顶点的变化求解更简便.

练习册系列答案
相关题目
19.已知A=$\frac{x}{y(x-y)}-\frac{y}{x(x-y)}$.
(1)化简A;
(2)已知$\frac{1}{x}+\frac{1}{y}=\sqrt{5}$(x≠y),求A的值.
(1)化简A;
(2)已知$\frac{1}{x}+\frac{1}{y}=\sqrt{5}$(x≠y),求A的值.
9.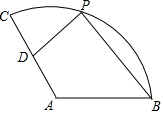 如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为$\widehat{BC}$上一动点(不与C,B重合),则2PD+PB的最小值为( )
如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为$\widehat{BC}$上一动点(不与C,B重合),则2PD+PB的最小值为( )
 如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为$\widehat{BC}$上一动点(不与C,B重合),则2PD+PB的最小值为( )
如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为$\widehat{BC}$上一动点(不与C,B重合),则2PD+PB的最小值为( )| A. | 4+2$\sqrt{3}$ | B. | 4$\sqrt{7}$ | C. | 10 | D. | 4$\sqrt{3}$+4 |
13.估计3+$\sqrt{10}$的运算结果应在( )
| A. | 3到4之间 | B. | 4到5之间 | C. | 5到6之间 | D. | 6到7之间 |
14.九(2)班体育委员用划记法统计本班40名同学投掷实心球的成绩,结果如图所示:则这40名同学投掷实心球的成绩的众数和中位数分别是( )
| 成绩 | 6 | 7 | 8 | 9 | 10 |
| 人数 |  | 正 一 | 正 正 一 | 正 正  | 正 |
| A. | 8,8 | B. | 8,8.5 | C. | 9,8 | D. | 9,8.5 |
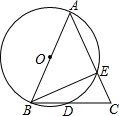 如图,△ABC中,AB=AC=10,BC=4$\sqrt{5}$,以AB为直径的⊙O分别交度BC,AC于点D、E.
如图,△ABC中,AB=AC=10,BC=4$\sqrt{5}$,以AB为直径的⊙O分别交度BC,AC于点D、E.