题目内容
15.关于x的一元二次方程x2+(2m-1)x-2m=0的两个正实数根分别为x1,x2,且x1+3x2=9,则m的值是-3或-$\frac{4}{3}$.分析 根据一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系和两根都为正根得到x1+x2=1-2m>0,x1•x2=-2m>0,则m<0,由x1+3x2=9得到1-2m+2x2=9,即x2=m+4,x1=-3m-3,于是有(-3m-3)(m+4)=-2m,然后解方程得到满足条件的m的值.
解答 解:根据题意得x1+x2=1-2m>0,x1•x2=-2m>0,
则m<0,
∵x1+3x2=9,
∴1-2m+2x2=9,即x2=m+4,
∴x1=-3m-3,
∴(-3m-3)(m+4)=-2m,
整理得3m2+13m+12=0,
(m+3)(3m+4)=0,
解得m1=-3,m2=-$\frac{4}{3}$,
m=-3或-$\frac{4}{3}$.
故答案为-3或-$\frac{4}{3}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两根分别为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了一元二次方程的解法.

练习册系列答案
相关题目
5.下列字母中,属于中心对称图形的是( )
| A. | D | B. | X | C. | V | D. | R |
3.在平面直角坐标系中,点A(3,m)在第四象限,若点A关于x轴的对称点B在直线y=-x+4上,则m的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
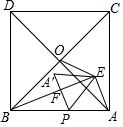 如图,在△ABE中,∠AEB=90°,AB=$\sqrt{29}$,以AB为边在△ABE的同侧作正方形ABCDD,点O是正方形对角线的交.点,连接OE,OE=$\frac{3}{2}$$\sqrt{2}$,点P为AB上一动点,将△APE沿直线PE翻折得到△A′PE,当A′P⊥BE于点F时,BF的长度是5-$\frac{10\sqrt{29}}{29}$.
如图,在△ABE中,∠AEB=90°,AB=$\sqrt{29}$,以AB为边在△ABE的同侧作正方形ABCDD,点O是正方形对角线的交.点,连接OE,OE=$\frac{3}{2}$$\sqrt{2}$,点P为AB上一动点,将△APE沿直线PE翻折得到△A′PE,当A′P⊥BE于点F时,BF的长度是5-$\frac{10\sqrt{29}}{29}$.
 如图所示,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F,
如图所示,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F,