题目内容
三个有理数a、b、c满足：a＜b＜c，且a+b+c=0，有下列各式：a，b，c，a+b，b+c，c+a．其中，哪些能够确定正负号？简述理由．
考点：有理数的加法,正数和负数
专题：
分析：三个数的和为0，且a＜b＜c，故三个数中最大的数为正，最小的数为负，而a+b=-c，b+c=-a，所以也可以确定．
解答：解：
a＜b＜c，且a+b+c=0
∴这三个数中最大的数为正，最小的数为负
∴a＜0，c＞0，b的符号不能确定
而a+b=-c，c为正数，所以a+b为负；
同理b+c为正，c+a不确定．
所以a为负，c为正，a+b这负，b+c为正，b和c+a不确定．
a＜b＜c，且a+b+c=0
∴这三个数中最大的数为正，最小的数为负
∴a＜0，c＞0，b的符号不能确定
而a+b=-c，c为正数，所以a+b为负；
同理b+c为正，c+a不确定．
所以a为负，c为正，a+b这负，b+c为正，b和c+a不确定．
点评：本题主要考查有理数的加法中符号的确定，解题的关键是对a+b+c=0进行转化．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，MN⊥AB于M，AM=8cm，AC=
已知等腰Rt△ABC和等腰Rt△AED中，∠AED=∠ACB=90°，点D在AB上，M为DB的中点，连接EC，N是EC的中点，连接DN并延长交AC于点F．求证：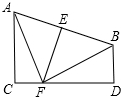
已知：如图所示，AC⊥CD，BD⊥CD．线段AB的垂直平分线EF交AB于点E，交CD于点F，且AC=FD=3，CF=1求线段AB的长度．
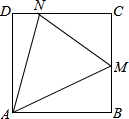如图，正方形ABCD中，M、N分别为BC和CD边上的两点，∠MAN=45°．