题目内容
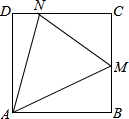 如图,正方形ABCD中,M、N分别为BC和CD边上的两点,∠MAN=45°.
如图,正方形ABCD中,M、N分别为BC和CD边上的两点,∠MAN=45°.(1)求证:BM+DN=MN;
(2)若AB=6,MN=5,求BM的长和△CMN的面积.
考点:正方形的性质,全等三角形的判定与性质,勾股定理
专题:
分析:(1)将△ABM绕点A逆时针旋转90°得到△ADE,根据旋转的性质可得AE=AM,BM=DE,∠DAE=∠BAM,然后求出∠EAN=∠MAN=45°,然后利用“边角边”证明△AMN和△AEN全等,根据全等三角形对应边相等可得MN=EN,再根据DE+DN=EN等量代换即可得证;
(2)设BM=x,表示出CM、DN、CN,然后利用勾股定理列出方程求解得到x,再利用三角形的面积列式计算即可得解.
(2)设BM=x,表示出CM、DN、CN,然后利用勾股定理列出方程求解得到x,再利用三角形的面积列式计算即可得解.
解答: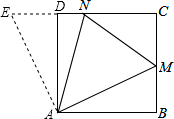 (1)证明:如图,将△ABM绕点A逆时针旋转90°得到△ADE,
(1)证明:如图,将△ABM绕点A逆时针旋转90°得到△ADE,
由旋转的性质得,AE=AM,BM=DE,∠DAE=∠BAM,
∵∠MAN=45°,
∴∠EAN=∠DAE+∠DAN=∠BAM+∠DAN=90°-45°=45°,
∴∠EAN=∠MAN=45°,
在△AMN和△AEN中,
,
∴△AMN≌△AEN(SAS),
∴MN=EN,
∵DE+DN=EN,
∴BM+DN=MN;
(2)解:设BM=x,则CM=6-x,DN=5-x,CN=6-(5-x)=x+1,
在Rt△MNC中,CN2+CM2=MN2,
即(x+1)2+(6-x)2=52,
整理得,x2-5x+6=0,
解得x1=2,x2=3,
∴BM的长为2或3;
当BM=2时,CM=6-2=4,CN=2+1=3,
△CMN的面积=
×3×4=6,
当BM=3时,CM=6-3=3,CN=3+1=4,
△CMN的面积=
×3×4=6.
综上所述,BM的长为2或3,△CMN的面积是6.
 (1)证明:如图,将△ABM绕点A逆时针旋转90°得到△ADE,
(1)证明:如图,将△ABM绕点A逆时针旋转90°得到△ADE,由旋转的性质得,AE=AM,BM=DE,∠DAE=∠BAM,
∵∠MAN=45°,
∴∠EAN=∠DAE+∠DAN=∠BAM+∠DAN=90°-45°=45°,
∴∠EAN=∠MAN=45°,
在△AMN和△AEN中,
|
∴△AMN≌△AEN(SAS),
∴MN=EN,
∵DE+DN=EN,
∴BM+DN=MN;
(2)解:设BM=x,则CM=6-x,DN=5-x,CN=6-(5-x)=x+1,
在Rt△MNC中,CN2+CM2=MN2,
即(x+1)2+(6-x)2=52,
整理得,x2-5x+6=0,
解得x1=2,x2=3,
∴BM的长为2或3;
当BM=2时,CM=6-2=4,CN=2+1=3,
△CMN的面积=
| 1 |
| 2 |
当BM=3时,CM=6-3=3,CN=3+1=4,
△CMN的面积=
| 1 |
| 2 |
综上所述,BM的长为2或3,△CMN的面积是6.
点评:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,熟记正方形的性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
 如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.
如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.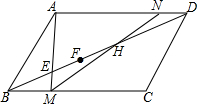 在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND=
在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND=