题目内容
 已知等腰Rt△ABC和等腰Rt△AED中,∠AED=∠ACB=90°,点D在AB上,M为DB的中点,连接EC,N是EC的中点,连接DN并延长交AC于点F.求证:
已知等腰Rt△ABC和等腰Rt△AED中,∠AED=∠ACB=90°,点D在AB上,M为DB的中点,连接EC,N是EC的中点,连接DN并延长交AC于点F.求证:(1)△EDN≌△CFN;
(2)MN=
| 1 |
| 2 |
考点:全等三角形的判定与性质,等腰直角三角形,三角形中位线定理
专题:证明题
分析:(1)根据等腰直角三角形的性质可得∠EAD=∠EDA=∠BAC=∠ABC=45°,∠EAC=90°,然后求出ED∥FC,根据两直线平行,内错角相等可得∠EDN=∠CFN,再利用“角角边”证明△EDN和△CFN全等即可;
(2)连接EM并延长到H,使EM=MH,连接CH、CH、BH,利用“边角边”证明△EDM和△FBM全等,根据全等三角形对应边相等可得BH=DE=AE,全等三角形对应角相等可得∠HBM=∠EDM=135°,再利用“边角边”证明△EAC和△HBC全等,根据全等三角形对应边相等可得HC=CE,然后根据三角形的中位线平行于第三边并且等于第三边的一半证明即可.
(2)连接EM并延长到H,使EM=MH,连接CH、CH、BH,利用“边角边”证明△EDM和△FBM全等,根据全等三角形对应边相等可得BH=DE=AE,全等三角形对应角相等可得∠HBM=∠EDM=135°,再利用“边角边”证明△EAC和△HBC全等,根据全等三角形对应边相等可得HC=CE,然后根据三角形的中位线平行于第三边并且等于第三边的一半证明即可.
解答:证明:(1)∵△ABC是等腰Rt△ABC和△AED是等腰Rt△AED,∠AED=∠ACB=90°,
∴∠EAD=∠EDA=∠BAC=∠ABC=45°,
∴∠EAC=90°,
∴ED∥FC,
∴∠EDN=∠CFN,
∵N是EC的中点,
∴EN=CN,
在△EDN和△CFN中
,
∴△EDN≌△CFN(AAS);
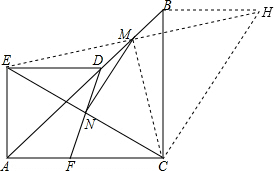
(2)连接EM并延长到H,使EM=MH,连接CH、CH、BH,
在△EDM和△FBM中,
,
∴△EDM≌△HBM(SAS),
∴BH=DE=AE,∠HBM=∠EDM=135°,
∴∠HBC=∠EAC=90°,
在△EAC和△HBC中,
,
∴△EAC≌△FBC(SAS),
∴HC=CE,
又∵点M、N分别是EH、EC的中点,
∴MN=
HC,
∴MN=
CE.
∴∠EAD=∠EDA=∠BAC=∠ABC=45°,
∴∠EAC=90°,
∴ED∥FC,
∴∠EDN=∠CFN,
∵N是EC的中点,
∴EN=CN,
在△EDN和△CFN中
|
∴△EDN≌△CFN(AAS);

(2)连接EM并延长到H,使EM=MH,连接CH、CH、BH,
在△EDM和△FBM中,
|
∴△EDM≌△HBM(SAS),
∴BH=DE=AE,∠HBM=∠EDM=135°,
∴∠HBC=∠EAC=90°,
在△EAC和△HBC中,
|
∴△EAC≌△FBC(SAS),
∴HC=CE,
又∵点M、N分别是EH、EC的中点,
∴MN=
| 1 |
| 2 |
∴MN=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,三角形的中位线平行于第三边并且等于第三边的一半,难点在于(2)作辅助线构造出全等三角形和以MN为中位线的三角形.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
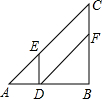 如图,在Rt△ABC中,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,问点D出发几秒后四边形DFCE的面积是△ABC面积的一半?
如图,在Rt△ABC中,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,问点D出发几秒后四边形DFCE的面积是△ABC面积的一半?