题目内容
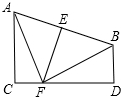 已知:如图所示,AC⊥CD,BD⊥CD.线段AB的垂直平分线EF交AB于点E,交CD于点F,且AC=FD=3,CF=1求线段AB的长度.
已知:如图所示,AC⊥CD,BD⊥CD.线段AB的垂直平分线EF交AB于点E,交CD于点F,且AC=FD=3,CF=1求线段AB的长度.考点:全等三角形的判定与性质,线段垂直平分线的性质,勾股定理
专题:
分析:根据线段垂直平分线上的点到两端点的距离相等可得AF=BF,再利用“HL”证明Rt△ACF与Rt△FDB全等,根据全等三角形对应角相等可得∠CAF=∠DFB,然后求出∠AFB=90°,再利用勾股定理列式求出AF,然后利用勾股定理列式计算即可得解.
解答:解:∵EF是AB的垂直平分线,
∴FA=FB,
∵AC⊥CD,BD⊥CD,
∴△ACF与△FDB是直角三角形.
在Rt△ACF与Rt△FDB中,
,
∴Rt△ACF≌Rt△FDB(HL),
∴∠CAF=∠DFB,
∵∠C=90°,
∴∠CAF+∠CFA=90°,
∴∠CFA+∠BFD=90°,
∴∠AFB=90°,
∴△ABF是等腰直角三角形.
∵AC=3,CF=1,
∴AF2=AC2+CF2=32+12=10,
∴AB=
=
=2
.
∴FA=FB,
∵AC⊥CD,BD⊥CD,
∴△ACF与△FDB是直角三角形.
在Rt△ACF与Rt△FDB中,
|
∴Rt△ACF≌Rt△FDB(HL),
∴∠CAF=∠DFB,
∵∠C=90°,
∴∠CAF+∠CFA=90°,
∴∠CFA+∠BFD=90°,
∴∠AFB=90°,
∴△ABF是等腰直角三角形.
∵AC=3,CF=1,
∴AF2=AC2+CF2=32+12=10,
∴AB=
| AF2+BF2 |
| 10+10 |
| 5 |
点评:本题考查了全等三角形的判定与性质,线段垂直平分线上的点到两端点的距离相等的性质,等腰直角三角形的判定与性质,勾股定理,熟练掌握三角形全等的判定方法并确定出全等三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
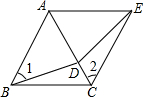 如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.
如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形. 如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.
如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.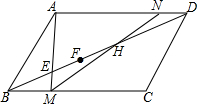 在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND=
在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND= 如图,把∠1,∠2,∠3按从大到小的顺序排列为
如图,把∠1,∠2,∠3按从大到小的顺序排列为