题目内容
阅读下列材料,回答后面的问题:
解方程|x-3|+5=2x
解:①若x-3>0,即x>3,则|x-3|=x-3;所以原方程变形x-3+5=2x,解得:
x=2,不符合x>3,故舍去.
②若x-3<0,即x<3,则|x-3|=3-x;所以原方程变形3-x+5=2x,解得:x=
,符合x>3.综上所述:x=
.
仿照上述解题思路解方程:|2x-4|=3x-1.
解方程|x-3|+5=2x
解:①若x-3>0,即x>3,则|x-3|=x-3;所以原方程变形x-3+5=2x,解得:
x=2,不符合x>3,故舍去.
②若x-3<0,即x<3,则|x-3|=3-x;所以原方程变形3-x+5=2x,解得:x=
| 8 |
| 3 |
| 8 |
| 3 |
仿照上述解题思路解方程:|2x-4|=3x-1.
考点:含绝对值符号的一元一次方程
专题:阅读型
分析:分类讨论:把含绝对值的方程转化成不含绝对值的方程,根据解方程,可得答案.
解答:解:①若2x-4≥0,即x≥2,
则|2x-4|=3x-1;
原方程变形2x-4=3x-1,
解得:x=-3,不符合x≥2,故舍去;
②若2x-4<0,即x<2,
则原方程变形-2x+4=3x-1,
解得:x=1,符合x<2.
综上所述:x=1.
则|2x-4|=3x-1;
原方程变形2x-4=3x-1,
解得:x=-3,不符合x≥2,故舍去;
②若2x-4<0,即x<2,
则原方程变形-2x+4=3x-1,
解得:x=1,符合x<2.
综上所述:x=1.
点评:本题考查了含绝对值符号的一元一次方程,利用了分类讨论的思想.

练习册系列答案
相关题目
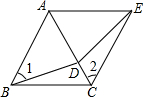 如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.
如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.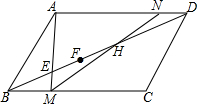 在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND=
在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND=