题目内容
 如图,在Rt△ABC中,∠C=90°,MN⊥AB于M,AM=8cm,AC=
如图,在Rt△ABC中,∠C=90°,MN⊥AB于M,AM=8cm,AC=| 4 |
| 5 |
考点:相似三角形的判定与性质
专题:
分析:∠C=90°,MN⊥AB,且∠A为公共角,所以△AMN∽△ACB,AC=
AB,所以可知AM=
AN,在Rt△AMN中,AM=8cm,则AN=10cm,由勾股定理可求得MN=6cm,可求得S△AMN=24cm2,且BC=15cm,所以
=(
)2=
,所以S△ABC=150cm2,所以四边形BCNM的面积为126cm2.
| 4 |
| 5 |
| 4 |
| 5 |
| S△AMN |
| S△ACB |
| MN |
| BC |
| 4 |
| 25 |
解答:解:∵MN⊥AB,
∴∠C=∠NMA=90°,且∠A为公共角,
∴△AMN∽△ACB,
∵AC=
AB,
∴AM=
AN,
在Rt△AMN中,AM=8cm,则AN=10cm,由勾股定理可求得MN=6cm,
∴S△AMN=24cm2,且BC=15cm,
∴
=(
)2=
,
∴S△ABC=150cm2,
∴四边形BCNM的面积为126cm2.
∴∠C=∠NMA=90°,且∠A为公共角,
∴△AMN∽△ACB,
∵AC=
| 4 |
| 5 |
∴AM=
| 4 |
| 5 |
在Rt△AMN中,AM=8cm,则AN=10cm,由勾股定理可求得MN=6cm,
∴S△AMN=24cm2,且BC=15cm,
∴
| S△AMN |
| S△ACB |
| MN |
| BC |
| 4 |
| 25 |
∴S△ABC=150cm2,
∴四边形BCNM的面积为126cm2.
点评:本题主要考查相似三角形的判定和性质,解题的关键是求出两三角形的相似比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在一块长35米,宽26米的矩形地面上,修建同样宽的道路如图所示(每个拐角都是直角),剩余部分栽种花草,要使剩余部分的面积为850平方米,道路的宽应为多少?
在一块长35米,宽26米的矩形地面上,修建同样宽的道路如图所示(每个拐角都是直角),剩余部分栽种花草,要使剩余部分的面积为850平方米,道路的宽应为多少?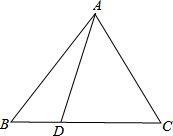 如图,在△ABC中,AB=AC,D为BC上任意一点,求证:AD2+BD•DC=AB2.
如图,在△ABC中,AB=AC,D为BC上任意一点,求证:AD2+BD•DC=AB2.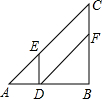 如图,在Rt△ABC中,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,问点D出发几秒后四边形DFCE的面积是△ABC面积的一半?
如图,在Rt△ABC中,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,问点D出发几秒后四边形DFCE的面积是△ABC面积的一半?