题目内容
一圆柱形油罐,其底面直径为5米,高为8米,要从A点环绕油罐建造梯子,正好到A点的正上方B点,则梯子最短需要 .(π取3)
考点:平面展开-最短路径问题
专题:
分析:将圆柱展开,得到矩形,求出矩形对角线即为梯子最短需要的距离.
解答: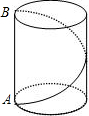
 解:如图,∵油罐的底面直径为5米,
解:如图,∵油罐的底面直径为5米,
∴油罐的底面周长为5π米=15米,
又∵高AB为8米,即展开图中BC=8米,
∴AB=
=17(米).
所以梯子最短需要17米.
故答案为17米.

 解:如图,∵油罐的底面直径为5米,
解:如图,∵油罐的底面直径为5米,∴油罐的底面周长为5π米=15米,
又∵高AB为8米,即展开图中BC=8米,
∴AB=
| 152+82 |
所以梯子最短需要17米.
故答案为17米.
点评:此题考查了平面展开--最短路径问题,关键是将圆柱展开为矩形,根据“两点之间线段最短”求出对角线长即可.

练习册系列答案
相关题目
已知a,b为两个连续整数,且a<
<b,则a+b值分别为( )
| 31 |
| A、7 | B、9 | C、11 | D、13 |
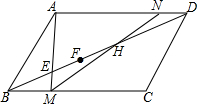 在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND=
在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND= 如图,把∠1,∠2,∠3按从大到小的顺序排列为
如图,把∠1,∠2,∠3按从大到小的顺序排列为