题目内容
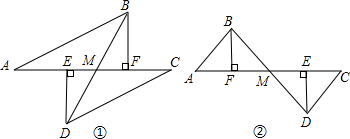
如图，正六边形ABCDEF内接于⊙O，P为弧BC上一点，试判断PC，PA，PB之间的数量关系，并证明．考点：正多边形和圆
专题：
分析：在AP上截取AQ=PC，连接BQ，根据SAS定理得出△ABQ≌△CBP，故可得出BQ=BP，由∠APB=30°即可得出PQ=
PB，由此得出结论．
| 3 |
解答：解：
PA=PC+
PB，
证明：在AP上截取AQ=PC，连接BQ，
在△ABQ和△CBP中，
，
∴△ABQ≌△CBP（SAS），
∴BQ=BP，
∵∠APB=30°，
∴PQ=
PB，
∴PA=PC+
PB．
PA=PC+| 3 |
证明：在AP上截取AQ=PC，连接BQ，
在△ABQ和△CBP中，
|
∴△ABQ≌△CBP（SAS），
∴BQ=BP，
∵∠APB=30°，
∴PQ=
| 3 |
∴PA=PC+
| 3 |
点评：本题考查的是正多边形和圆，熟知正六边形的性质是解答此题的关键．
练习册系列答案
相关题目
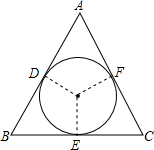如图，在△ABC中，AB=AC，⊙O是△ABC的内切圆，它与AB，BC，CA分别相切于点D、E、F．若∠ACB=90°，AB=AC=2，求圆的半径．
已知：如图，AB是⊙O直径，弦CD⊥AB，E为CD延长线上一点，连结BE交圆于F．求证：CF•DE=BC•EF．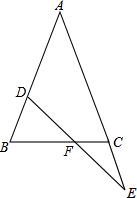
如图，△ABC中，AB=AC，点D在AB上，点E在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CE．