题目内容
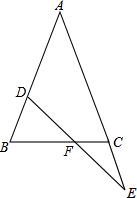 如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE.
如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE.考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:如图,作辅助线;证明△DGF∽△ECF,得到DG=CE,此为解决该问题的关键性结论;证明BD=GD,即可解决问题.
解答: 证明:如图,过点D作DG∥AE,交BC于点G;
证明:如图,过点D作DG∥AE,交BC于点G;
则△DGF∽△ECF,
∴DG:CE=DF:EF,而DF=EF,
∴DG=CE;
∵AB=AC,
∴∠B=∠ACB;
∵DG∥AE,
∴∠DGB=∠ACB,
∴∠DBG=∠DGB,
∴DG=BD,
∴BD=CE.
 证明:如图,过点D作DG∥AE,交BC于点G;
证明:如图,过点D作DG∥AE,交BC于点G;则△DGF∽△ECF,
∴DG:CE=DF:EF,而DF=EF,
∴DG=CE;
∵AB=AC,
∴∠B=∠ACB;
∵DG∥AE,
∴∠DGB=∠ACB,
∴∠DBG=∠DGB,
∴DG=BD,
∴BD=CE.
点评:该题主要考查了等腰三角形的判定及其应用、相似三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造相似三角形.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,正六边形ABCDEF内接于⊙O,P为弧BC上一点,试判断PC,PA,PB之间的数量关系,并证明.
如图,正六边形ABCDEF内接于⊙O,P为弧BC上一点,试判断PC,PA,PB之间的数量关系,并证明.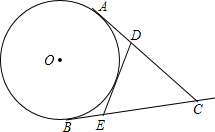 AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系.
AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系.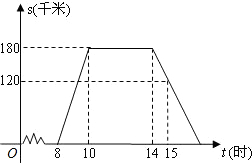 “国庆黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的折线表示.根据图象提供的有关信息,解答下列问题:
“国庆黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的折线表示.根据图象提供的有关信息,解答下列问题: 如图,在直角坐标系中,每个小正方形的边长都是单位1.
如图,在直角坐标系中,每个小正方形的边长都是单位1.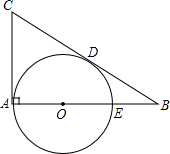 如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )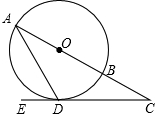 如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.
如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.