题目内容
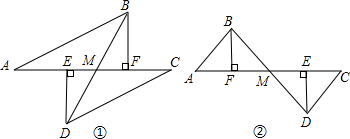
如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.
(1)求证:MB=MD,AM=CM;
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
(1)求证:MB=MD,AM=CM;
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.

考点:全等三角形的判定与性质
专题:
分析:(1)易证AE=CF,RT△ABF≌RT△CDE,可得BF=DE,即可证明△DEM≌△BFM,可得EM=FM,DM=BM,即可解题;
(2)易证RT△ABF≌RT△CDE,可得BF=DE,即可证明△DEM≌△BFM,可得EM=FM,DM=BM,即可解题.
(2)易证RT△ABF≌RT△CDE,可得BF=DE,即可证明△DEM≌△BFM,可得EM=FM,DM=BM,即可解题.
解答:证明:(1)∵AF=CE,∴AE=CF,
在RT△ABF和RT△CDE中,
,
∴RT△ABF≌RT△CDE(HL),
∴BF=DE,
在△DEM和△BFM中,
,
∴△DEM≌△BFM,(AAS)
∴EM=FM,DM=BM,
∴MB=MD,AM=CM;
(2)在RT△ABF和RT△CDE中,
,
∴RT△ABF≌RT△CDE(HL),
∴BF=DE,
在△DEM和△BFM中,
,
∴△DEM≌△BFM(AAS),
∴EM=FM,DM=BM,
∴MB=MD,AM=CM.
在RT△ABF和RT△CDE中,
|
∴RT△ABF≌RT△CDE(HL),
∴BF=DE,
在△DEM和△BFM中,
|
∴△DEM≌△BFM,(AAS)
∴EM=FM,DM=BM,
∴MB=MD,AM=CM;
(2)在RT△ABF和RT△CDE中,
|
∴RT△ABF≌RT△CDE(HL),
∴BF=DE,
在△DEM和△BFM中,
|
∴△DEM≌△BFM(AAS),
∴EM=FM,DM=BM,
∴MB=MD,AM=CM.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证RT△ABF≌RT△CDE和△DEM≌△BFM是解题的关键.

练习册系列答案
相关题目
下列运算错误的是( )
| A、(-a)(-a)=(-a)2 |
| B、-32•(-3)4=(-3)6 |
| C、(-a)3•(-a)2=(-a)5 |
| D、(-a)3•(-a)3=a6 |
 如图,正六边形ABCDEF内接于⊙O,P为弧BC上一点,试判断PC,PA,PB之间的数量关系,并证明.
如图,正六边形ABCDEF内接于⊙O,P为弧BC上一点,试判断PC,PA,PB之间的数量关系,并证明.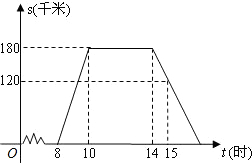 “国庆黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的折线表示.根据图象提供的有关信息,解答下列问题:
“国庆黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的折线表示.根据图象提供的有关信息,解答下列问题: 如图,在直角坐标系中,每个小正方形的边长都是单位1.
如图,在直角坐标系中,每个小正方形的边长都是单位1.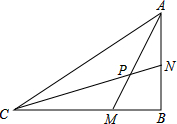 如图,△ABC是直角三角形,CM=AB,BM=AN,求∠CPM.
如图,△ABC是直角三角形,CM=AB,BM=AN,求∠CPM.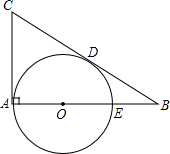 如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )