题目内容
13. 如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°(1)求证:∠BAG=∠CBF;
(2)求证:AG=FG;
(3)若GF=2BG,CF=$\sqrt{2}$,求AB的长.
分析 (1)根据同角的余角相等即可证明;
(2)过C点作CH⊥BF于H点,根据已知条件可证明△AGB≌△BHC,所以AG=BH,BG=CH,又因为BH=BG+GH,所以可得BH=HF+GH=FG,进而证明AG=FG;
(3)在Rt△ABG中,分别求出BG、AG即可解决问题;
解答 (1)证明:过C点作CH⊥BF于H点,
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°
∴∠BAG=∠FBE,
(2)证明:∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,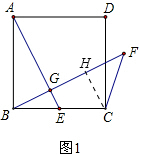
在△AGB和△BHC中,
$\left\{\begin{array}{l}{∠AGB=∠BHC}\\{∠BAG=∠HBC}\\{AB=BC}\end{array}\right.$,
∴△AGB≌△BHC,
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
(3)解:在Rt△CHF中,∠CFB=45°,
∵CF=$\sqrt{2}$,
∴CH=FH=1,
由(2)可知BG=CH,AG=FG,
∴BG=1,∵GF=2BG,
∴FG=AG=2,
在Rt△ABG中,AB=$\sqrt{A{G}^{2}+B{G}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
点评 本题考查了正方形的性质、全等三角形的判定和性质以及勾股定理的运用,题目的综合性很强,对学生的解题要求能力很高.

练习册系列答案
相关题目
1.2-2等于( )
| A. | -$\frac{1}{4}$ | B. | -4 | C. | 4 | D. | $\frac{1}{4}$ |
18.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为($\sqrt{2}$+$\sqrt{6}$)cm.
一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为($\sqrt{2}$+$\sqrt{6}$)cm.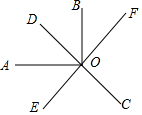 如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°.
如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°. 如图,△ABC中,AB=AC,BC=3,AD是BC边上的高,且AD=4,则图中阴影部分的面积为3.
如图,△ABC中,AB=AC,BC=3,AD是BC边上的高,且AD=4,则图中阴影部分的面积为3.