题目内容
3．解不等式组$\left\{\begin{array}{l}{1-3（x-1）≤8-x}\\{\frac{x+3}{2}+\frac{x-1}{3}＞x+1}\end{array}\right.$并把解集表示在数轴上．分析 先求出每个不等式的解集，再求出不等式组的解集即可．
解答 解：$\left\{\begin{array}{l}{1-3（x-1）≤8-x①}\\{\frac{x+3}{2}+\frac{x-1}{3}＞x+1②}\end{array}\right.$
∵解不等式①得：x≥-2，
解不等式②得：x＜1，
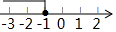
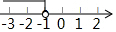
∴不等式组的解集为-2≤x＜1，
在数轴上表示为：
．
点评 本题考查了解一元一次不等式组和在数轴上表示不等式组的解集，能根据不等式的解集求出不等式组的解集是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，正方形ABCD中，E为BC上一点，过B作BG⊥AE于G，延长BG至点F使∠CFB=45°
在如图的平面直角坐标系中，点A，B，C都在正方形网格的格点上，且每个小正方形的边长为1．
18．已知$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$和$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$都是方程y=kx+b的解，则k和b的值是（ ）
| A． | $\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=5}\end{array}\right.$ |
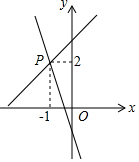如图，己知直线y1=x+m与y2=kx-1相交于点P（-1，2），则关于x的不等式x+m＜kx-1的解集在数轴上表示正确的是（ ）
