题目内容

18．利用公式法分解因式求使4x2-12x+9y2+30y+35的值为1时x，y的值．

分析 根据题意得4x2-12x+9y2+30y+34=0，因式分解后结合非负数性质可得x、y的值．

解答 解：根据题意得：4x2-12x+9y2+30y+35=1，
即：4x2-12x+9y2+30y+34=0，
因式分解得，（2x-3）2+（3y+5）2=0，
∴2x-3=0，3y+5=0，
解得：x=$\frac{3}{2}$，y=-$\frac{5}{3}$．

点评 本题主要考查公式法分解因式的能力，根据题意列出方程是前提，因式分解是解题的关键．

练习册系列答案
相关题目
8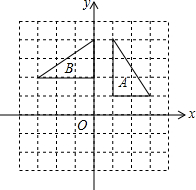．如图，在边长为1的正方形网格中，图形B是由图形A旋转得到的，则旋转中心的坐标为（　　）
A．（0，1）B．（-1，0）C．（0，0）D．（-2，-1）
9．甲、乙两名同学从《奔跑吧兄弟》、《极限挑战》、《最强大脑》三个综艺节目中随机选择一个观看．
（1）甲同学观看《最强大脑》的概率是$\frac{1}{3}$；
（2）求甲、乙两名同学观看同一节目的概率．
6．解方程组：$\left\{\begin{array}{l}{2x+y=4，①}\\{x+3z=1，②}\\{x+y+z=7．③}\end{array}\right.$．
13．如图，在平面直角坐标系xOy中，双曲线y1=$\frac{2}{x}$
（1）当x＞0时，y1＞0；
（2）直线y2=-x+b，当b=2$\sqrt{2}$时，直线与双曲线有唯一公共点，问：bb＞2$\sqrt{2}$或b＜-2$\sqrt{2}$时，直线与双曲线有两个公共点；
（3）如果直线y2=-x+b与双曲线y1=$\frac{2}{x}$交于A、B两点，且点A的坐标为（1，2），点B的纵坐标为1．设E为线段AB的中点，过点E作x轴的垂线EF，交双曲线于点F．求线段EF的长．
3．写出一个最简分式使它满足：含有字母x，y；无论x，y为何值时，分式的值一定是负的，符合这两个条件的分式可以是-$\frac{1}{{x}^{2}+{y}^{2}+1}$．
10．二元一次方程组$\left\{\begin{array}{l}{2x-y=10}\\{y=-3x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=-6}\end{array}\right.$．
9．如图1，在直角坐标系中，点B（a，b）在第一象限，且$\sqrt{a-4}$+b2-8b+16=0，过B作x轴，y轴的垂线分别交于A、C．

（1）求B的坐标和四边形OABC的面积．
（2）直线y=2x+8交x轴于E，交y轴于F，它沿x轴正方向以每秒移动1个单位的速度，设平移的时间为t秒，问是否存在t的值，使直线EF平分四边形OABC的面积？若存在，求t的值；若不存在，说明理由．
（3）如图2，P为正方形OABC的多角线AC上的点（端点A，C除外），PM⊥PO，交直线AB于M，问$\frac{PC}{BM}$的值是否不变？请给出结论，予以证明并求其值．
10．若关于x的不等式$\frac{2x+3}{2}$＞2x+$\frac{m}{2}$的正整数解为1，2，3，则m的取值范围（　　）
A．-7＜m≤-5B．-7≤m＜-5C．-5＜m≤-3D．-5≤m＜-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网