题目内容
10．若关于x的不等式$\frac{2x+3}{2}$＞2x+$\frac{m}{2}$的正整数解为1，2，3，则m的取值范围（ ）| A． | -7＜m≤-5 | B． | -7≤m＜-5 | C． | -5＜m≤-3 | D． | -5≤m＜-3 |
分析 先表示出不等式$\frac{2x+3}{2}$＞2x+$\frac{m}{2}$的解集，再由正整数解为1、2、3，可得出$3＜\frac{3-m}{2}≤4$，解出即可．
解答 解：解不等式得：x＜$\frac{3-m}{2}$，
∵不等式的正整数解为1、2、3，
∴$3＜\frac{3-m}{2}≤4$，
解得：-5≤m＜-3，
故选：D．
点评 本题考查了一元一次不等式的整数解，解答本题的关键是得出关于m的不等式．
练习册系列答案
相关题目
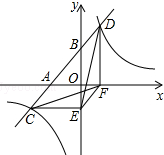如图，一次函数y=ax+b与x轴、y轴交于A、B两点，与反比例函数y=$\frac{k}{x}$相交于C、D两点，分别过C、D两点作y轴、x轴的垂线，垂足为E、F，连接CF、DE、EF． 有下列三个结论：①△CEF与△DEF的面积相等；②△DCE≌△CDF；③AC=BD．其中正确的结论个数是（ ）
15．已知x＞4，下列说法中错误的个数有（ ）
①不等式有无数个解；②-x＜-4；③1010是不等式的解；④x可以取4．
①不等式有无数个解；②-x＜-4；③1010是不等式的解；④x可以取4．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，在?ABCD中，AB=AC，若?ABCD的周长为38，△ABC的周长比?ABCD的周长少10，求AB和BC的长．
如图，在?ABCD中，AE是∠BAD的平分线交DC于点E，求证：CE+BC=AB．