题目内容
13. 如图,在平面直角坐标系xOy中,双曲线y1=$\frac{2}{x}$
如图,在平面直角坐标系xOy中,双曲线y1=$\frac{2}{x}$(1)当x>0时,y1>0;
(2)直线y2=-x+b,当b=2$\sqrt{2}$时,直线与双曲线有唯一公共点,问:bb>2$\sqrt{2}$或b<-2$\sqrt{2}$时,直线与双曲线有两个公共点;
(3)如果直线y2=-x+b与双曲线y1=$\frac{2}{x}$交于A、B两点,且点A的坐标为(1,2),点B的纵坐标为1.设E为线段AB的中点,过点E作x轴的垂线EF,交双曲线于点F.求线段EF的长.
分析 (1)双曲线的图象落在x轴上方时,函数值大于0,根据图象可知此时x>0;
(2)将y=-x+b代入y=$\frac{2}{x}$,整理得出x2-bx+2=0,当△=b2-8>0时,直线与双曲线有两个公共点,解不等式即可;
(3)将y=1代入y1=$\frac{2}{x}$,求出x的值,得到点B的坐标,再根据中点坐标公式求出点E的坐标,将点E横坐标的值代入y1=$\frac{2}{x}$,求出点F纵坐标的值,进而求得线段EF的长.
解答 解:(1)根据图象可得x>0时,y1>0;
(2)将y=-x+b代入y=$\frac{2}{x}$,得$\frac{2}{x}$=-x+b,
整理得,x2-bx+2=0,
当△=b2-8>0时,直线与双曲线有两个公共点,
解得b>2$\sqrt{2}$或b<-2$\sqrt{2}$;
(3)将y=1代入y1=$\frac{2}{x}$,得x=2,则点B的坐标为(2,1),
∵点A的坐标为(1,2),E为线段AB的中点,
∴点E的坐标为($\frac{3}{2}$,$\frac{3}{2}$),
当x=$\frac{3}{2}$时,y1=$\frac{2}{x}$=$\frac{4}{3}$,
∴EF=$\frac{3}{2}$-$\frac{4}{3}$=$\frac{1}{6}$.
故答案为>0;b>2$\sqrt{2}$或b<-2$\sqrt{2}$.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了函数图象上点的坐标特征,线段中点坐标公式.

练习册系列答案
相关题目
1.下列语句中,不是命题的是( )
| A. | 两点之间线段最短 | B. | 连接A、B两点 | ||
| C. | 平行于同一直线的两直线平行 | D. | 相等的角都是直角 |
8.有五张形状、大小、质地都相同的卡片,这些卡片上面分别画有下列图形:①正方形;②等边三角形;③平行四边形;④等腰三角形;⑤圆.将卡片背面朝上洗匀,从中随机抽取一张,抽出的纸片正面图形是轴对称图形,但不是中心对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
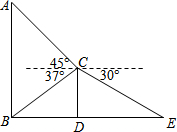 某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.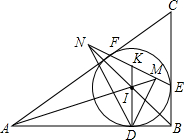 如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.
如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.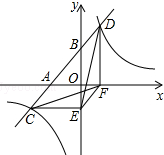 如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=$\frac{k}{x}$相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=$\frac{k}{x}$相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )