题目内容
6.解方程组:$\left\{\begin{array}{l}{2x+y=4,①}\\{x+3z=1,②}\\{x+y+z=7.③}\end{array}\right.$.分析 只需运用消元法先消去其中一个未知数,转化二元一次方程组,然后解这个方程组,就可解决问题.
解答 解:由③×3-②得:2x+3y=20④,
解①④组成的方程组,得
$\left\{\begin{array}{l}{2x+y=4}\\{2x+3y=20}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-2}\\{y=8}\end{array}\right.$,
把x=-2代入②得z=1,
∴原方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=8}\\{z=1}\end{array}\right.$.
点评 本题主要考查的是三元一次方程组的解法,在解题的过程中用到了转化思想、消元法等重要的数学思想方法,应熟练掌握.

练习册系列答案
相关题目
17. 如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠ACB=110°,则∠P的度数是( )
如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠ACB=110°,则∠P的度数是( )
 如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠ACB=110°,则∠P的度数是( )
如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠ACB=110°,则∠P的度数是( )| A. | 55° | B. | 30° | C. | 35° | D. | 40° |
1.下列语句中,不是命题的是( )
| A. | 两点之间线段最短 | B. | 连接A、B两点 | ||
| C. | 平行于同一直线的两直线平行 | D. | 相等的角都是直角 |
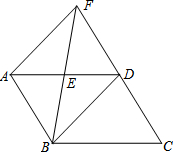 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.