Question

4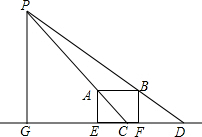．如图，操场边的路灯照在水平放置的单杠AB上，在地面上留下影子CD，经测量得知AB=1.8米，CD=3.24米，单杠高1.6米，试求路灯P的高度．

Answer 1

分析 先证明△PAB∽△PCD，则利用相似比可得$\frac{PA}{PC}$=$\frac{AB}{CD}$=$\frac{5}{9}$，再根据比例的性质得$\frac{CA}{CP}$=$\frac{4}{9}$，然后证明△CAE∽△CPG，于是可利用相似比可计算出PG．

解答 解：∵AB∥CD，
∴△PAB∽△PCD，
∴$\frac{PA}{PC}$=$\frac{AB}{CD}$=$\frac{1.8}{3.24}$=$\frac{5}{9}$，
∴$\frac{CA}{CP}$=$\frac{4}{9}$，
∵AE∥PG，
∴△CAE∽△CPG，
∴$\frac{AE}{PG}$=$\frac{CA}{CP}$，即$\frac{1.6}{PG}$=$\frac{4}{9}$，
∴PG=3.6（m）．
答：路灯P的高度为3.6m．

点评 本题考查了相似三角形的应用：常常构造“A”型或“X”型相似图，利用三角形相似的对应边成比例求相应线段的长．