题目内容
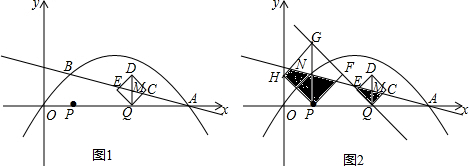
10.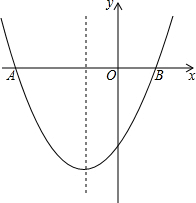 已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-2,与x轴交于A、B两点,与y轴交于点C,其中A(-6,0),C(0,-4).
已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-2,与x轴交于A、B两点,与y轴交于点C,其中A(-6,0),C(0,-4).(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得△PBC的周长最小.请求出点P的坐标.
(3)在第(2)问的基础上,若点D是线段OC上的一个动点(不与点O、点C重合).过点D作DE∥PC交x轴于点E.连接PD、PE.设CD的长为m,△PDE的面积为S.求S与m之间的函数关系式.试说明S是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据线段垂直平分线上的点到线段两端点的距离相等,可得PB=PA,根据两点间线段最短,可得CA与对称轴的交点P,根据自变量与函数值的对应关系,可得答案;
(3)根据相似三角形的判定与性质,可得OE=6-$\frac{3}{2}$m,根据图形分割法,可得二次函数解析式,根据二次函数的性质,可得答案.
解答 解:(1)1)将A、C点坐标代入函数解析式、对称轴的坐标公式,得
$\left\{\begin{array}{l}{-\frac{b}{2a}=-2}\\{36a-6b+c=0}\\{c=-4}\end{array}\right.$,
解得a$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=\frac{4}{3}}\\{c=-4}\end{array}\right.$
∴此抛物线的解析式为y=$\frac{1}{3}$x2+$\frac{4}{3}$x-4
(2) 连结AC、BC.因为BC的长度一定,所以△PBC周长最小,就是使PC+PB最小.
连结AC、BC.因为BC的长度一定,所以△PBC周长最小,就是使PC+PB最小.
B点关于对称轴的对称点是A点,AC与对称轴x=-2的交点即为所求的点P.
设直线AC的表达式为y=kx+b
则$\left\{\begin{array}{l}-6k+b=0\\ b=-4\end{array}\right.$
解得$\left\{\begin{array}{l}k=-\frac{2}{3}\\ b=-4\end{array}\right.$
∴此直线的表达式为y=-$\frac{2}{3}$x-4
把x=-2代入得y=-$\frac{8}{3}$
∴P点的坐标为(-2,-$\frac{8}{3}$)
(3)S存在最大值,
∵DE∥PC 即DE∥AC
∴△OED∽△OAC
∴$\frac{OD}{OC}=\frac{OE}{OA}$即$\frac{4-m}{4}$=$\frac{OE}{6}$
∴OE=6-$\frac{3}{2}$m,AE=6-OE=$\frac{3}{2}$m
连结OP ,
,
S=S△OAC-S△OED-S△AEP-S△PCD
=$\frac{1}{2}$×6×4-$\frac{1}{2}$×(6-$\frac{3}{2}$m)×(4-m)-$\frac{1}{2}$×$\frac{3}{2}$m×$\frac{8}{3}$-$\frac{1}{2}$×m×2
=-$\frac{3}{4}$m2+3m=$-\frac{3}{4}{(m-2)^2}+3$
∵-$\frac{3}{4}$<0
∴当m=2时,S最大=3
点评 本题考查了二次函数综合题,利用待定系数求函数解析式,利用线段的性质得出P点的位置,利用相似三角形的判定与性质得出OE=6-$\frac{3}{2}$m,利用图形割补法得出二次函数是解题关键,又利用了二次函数的性质.

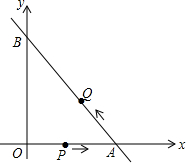
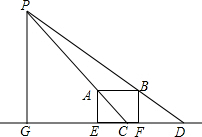 如图,操场边的路灯照在水平放置的单杠AB上,在地面上留下影子CD,经测量得知AB=1.8米,CD=3.24米,单杠高1.6米,试求路灯P的高度.
如图,操场边的路灯照在水平放置的单杠AB上,在地面上留下影子CD,经测量得知AB=1.8米,CD=3.24米,单杠高1.6米,试求路灯P的高度.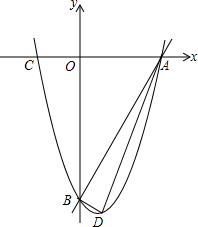 如图,已知一次函数y=2x-8与抛物线y=x2+bx+c都经过x轴上的A点和y轴上的B点.
如图,已知一次函数y=2x-8与抛物线y=x2+bx+c都经过x轴上的A点和y轴上的B点.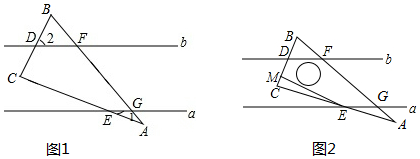
 如图,Rt△AOB的顶点A、B分别落在坐标轴上,O为原点,点A的坐标为(12,0),点B的坐标为(0,16),动点P从点O出发沿OA向终点A以每秒2个单位的速度运动,同时动点Q从点A出发,沿AB向终点B以每秒$\frac{10}{3}$个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动,设动点P、Q运动的时间为t秒(t>0).
如图,Rt△AOB的顶点A、B分别落在坐标轴上,O为原点,点A的坐标为(12,0),点B的坐标为(0,16),动点P从点O出发沿OA向终点A以每秒2个单位的速度运动,同时动点Q从点A出发,沿AB向终点B以每秒$\frac{10}{3}$个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动,设动点P、Q运动的时间为t秒(t>0).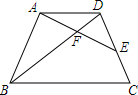 如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,点E在边CD上,AE与BD相交于点F,∠EAD=∠ABD.
如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,点E在边CD上,AE与BD相交于点F,∠EAD=∠ABD.