题目内容
16.计算(1+2+…+n-1)(2+3+…+n)-(2+3+…n-1)•(1+2+…+n)分析 设1+2+…+n-1=a,2+3+…n-1=b,则a-b=1,把原式化成a(b+n)-b(a+n),再去括号,合并同类项,即可得出结果.
解答 解:设1+2+…+n-1=a,2+3+…n-1=b,
则a-b=1,
∴(1+2+…+n-1)(2+3+…+n)-(2+3+…n-1)•(1+2+…+n)
=a(b+n)-b(a+n)
=ab+an-ab-bn
=an-bn
=n(a-b)
=n.
点评 本题考查了整式的混合运算与解题技巧方法;通过设出a和b再进行计算是解决问题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
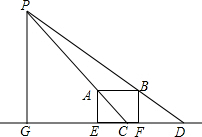 如图,操场边的路灯照在水平放置的单杠AB上,在地面上留下影子CD,经测量得知AB=1.8米,CD=3.24米,单杠高1.6米,试求路灯P的高度.
如图,操场边的路灯照在水平放置的单杠AB上,在地面上留下影子CD,经测量得知AB=1.8米,CD=3.24米,单杠高1.6米,试求路灯P的高度.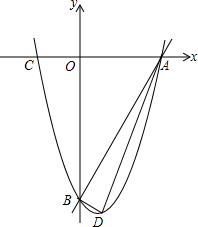 如图,已知一次函数y=2x-8与抛物线y=x2+bx+c都经过x轴上的A点和y轴上的B点.
如图,已知一次函数y=2x-8与抛物线y=x2+bx+c都经过x轴上的A点和y轴上的B点.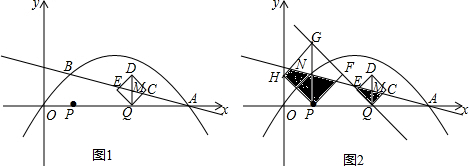
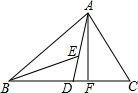 如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.