题目内容
6. 如图,已知C是AB的中点,AE=BD,∠A=∠B,求证:∠ACD=∠BCE.
如图,已知C是AB的中点,AE=BD,∠A=∠B,求证:∠ACD=∠BCE.
分析 易证AC=BC,即可证明△ACE≌△BCD,根据全等三角形对应角相等的性质即可得证.
解答 证明:∵C是AB的中点,
∴AC=BC,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AE=BD}\\{∠A=∠B}\\{AC=BC}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴∠ACE=∠BCD,
∴∠ACE-∠DCE=∠BCD-∠DCE,
即∠ACD=∠BCE.
点评 本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ACE≌△BCD是解题的关键.

练习册系列答案
相关题目
14.定义运算a□b=a(1-b),下面给出了关于这种运算的几个结论:
①2□(-2)=6;②a□b=b□a;③若a+b=0,则(a□a)+(b□b)=2ab;④若a□b=0,则a=0,
其中正确结论的个数( )
①2□(-2)=6;②a□b=b□a;③若a+b=0,则(a□a)+(b□b)=2ab;④若a□b=0,则a=0,
其中正确结论的个数( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.下列运算正确的是( )
| A. | a•a2=a2 | B. | (ab)2=ab2 | C. | (a2)3=a6 | D. | a10÷a2=a5 |
15.已知a-b=1,则a2-b2-2b的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
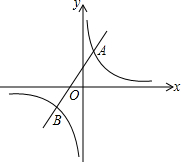 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)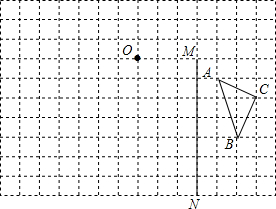 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).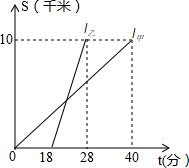 某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.
某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.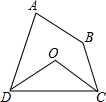 如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.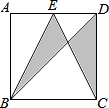 如图,正方形ABCD的边长为3,E为AD的中点,连接BE、BD、CE,则图中阴影部分的面积是3.
如图,正方形ABCD的边长为3,E为AD的中点,连接BE、BD、CE,则图中阴影部分的面积是3.