题目内容
18.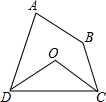 如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.
分析 首先根据四边形内角和可得∠ADC+∠DCB=360°-200°=160°,再根据角平分线的性质可得∠ODC+∠OCD=$\frac{1}{2}$×160°=80°,再进一步利用三角形内角和定理可得答案.
解答 解:∵四边形ABCD中,∠A+∠B=200°,
∴∠ADC+∠DCB=360°-200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=$\frac{1}{2}$∠ADC,∠OCD=$\frac{1}{2}$∠BCD,
∴∠ODC+∠OCD=$\frac{1}{2}$×160°=80°,
∴∠COD=180°-80°=100°.
点评 此题主要考查了多边形内角和定理,关键是掌握多边形内角和定理:(n-2).180 (n≥3)且n为整数).

练习册系列答案
相关题目
9.49的平方根是( )
| A. | 7 | B. | -7 | C. | ±7 | D. | $\sqrt{49}$ |
7.下列各式中,结果不等于2的是( )
| A. | 2-1 | B. | -(-2) | C. | $\sqrt{4}$ | D. | |-2| |
 如图,已知C是AB的中点,AE=BD,∠A=∠B,求证:∠ACD=∠BCE.
如图,已知C是AB的中点,AE=BD,∠A=∠B,求证:∠ACD=∠BCE. 请将下列证明过程补充完整:
请将下列证明过程补充完整: