题目内容
16.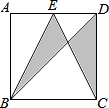 如图,正方形ABCD的边长为3,E为AD的中点,连接BE、BD、CE,则图中阴影部分的面积是3.
如图,正方形ABCD的边长为3,E为AD的中点,连接BE、BD、CE,则图中阴影部分的面积是3.
分析 CE与BD相交于F点,如图,由DE∥BC可判断△DEF∽△BCF,则$\frac{EF}{FC}$=$\frac{DF}{BF}$=$\frac{DE}{BC}$=$\frac{1}{2}$,于是利用三角形面积公式可得S△DCF=S△EBF=2S△DEF,而S△CDE=$\frac{9}{4}$,所以S△DCF=S△EBF=$\frac{2}{3}$×$\frac{9}{4}$=$\frac{3}{2}$,然后计算图中阴影部分的面积.
解答 解:CE与BD相交于F点,如图,
∵E为AD的中点,
∴DE=$\frac{3}{2}$,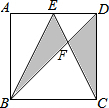
∵DE∥BC,
∴△DEF∽△BCF,
∴$\frac{EF}{FC}$=$\frac{DF}{BF}$=$\frac{DE}{BC}$=$\frac{1}{2}$,
∴S△DCF=S△EBF=2S△DEF,
而S△CDE=$\frac{1}{2}$×3×$\frac{3}{2}$=$\frac{9}{4}$,
∴S△DCF=S△EBF=$\frac{2}{3}$×$\frac{9}{4}$=$\frac{3}{2}$,
∴图中阴影部分的面积=2×$\frac{3}{2}$=3.
故答案为3.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了相似三角形的判定与性质和三角形面积公式.

练习册系列答案
相关题目
7.下列各式中,结果不等于2的是( )
| A. | 2-1 | B. | -(-2) | C. | $\sqrt{4}$ | D. | |-2| |
6.下列选项中是一元二次方程的是( )
| A. | 2x2+x-3 | B. | $\frac{5x}{{x}^{2}+1}$=2 | C. | x+2=0 | D. | t2-m=1-4t-m |
 如图,已知C是AB的中点,AE=BD,∠A=∠B,求证:∠ACD=∠BCE.
如图,已知C是AB的中点,AE=BD,∠A=∠B,求证:∠ACD=∠BCE.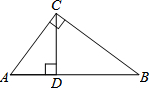 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=6,AB=9,则AD=( )
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=6,AB=9,则AD=( )