题目内容
10.已知抛物线y=x2+3x+c过两点(m,0)、(n,0),且m3+3m2+(c-2)m-2n-c=8,抛物线与双曲线$y=\frac{k}{x}$(x>0)的交点为(1,d).(1)求抛物线与双曲线的解析式;
(2)已知点P1,P2,…,P2012都在双曲线$y=\frac{k}{x}$(x>0)上,它们的横坐标分别为a,2a,…,2012a,O为坐标原点,记${S_1}={S_{△{P_1}{P_2}O}},{S_2}={S_{△{P_1}{P_3}O}},…$,点Q在双曲线$y=\frac{k}{x}$(x<0)上,过Q作QM⊥y轴于M,记S=S△QMO.求${S_1}+{S_2}+…+{S_{2011}}+\frac{S}{2}+\frac{S}{3}+…+\frac{S}{2012}$的值.
分析 (1)根据题意列出方程组,求出c的值,确定出抛物线解析式;根据题意求出k的值,即可确定出双曲线解析式;
(2)根据点P1,P2,…,P2012都在双曲线$y=\frac{k}{x}$(x>0)上,它们的横坐标分别为a,2a,…,2012a,分别求出纵坐标,如图,过P1、Pn+1分别作x轴、y轴的平行线,根据题意表示出Sn,再由Q在双曲线y=$\frac{k}{x}$上,得到S=S△QMO=1,即可求出所求式子的值.
解答 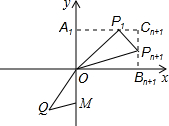 解:(1)$\left\{\begin{array}{l}m({m^2}+3m+c)-2(m+n)-c=8\\{m^2}+3m+c=0\\ m+n=-3\end{array}\right.$,
解:(1)$\left\{\begin{array}{l}m({m^2}+3m+c)-2(m+n)-c=8\\{m^2}+3m+c=0\\ m+n=-3\end{array}\right.$,
解得:c=-2,
∴y=x2+3x-2;
由$\left\{\begin{array}{l}{d=1+3-2}\\{d=\frac{k}{1}}\end{array}\right.$,得到$\left\{\begin{array}{l}{d=2}\\{k=2}\end{array}\right.$,
∴y=$\frac{2}{x}$;
(2)∵点P1,Pn+1(n=1,2,…,2011)都在双曲线$y=\frac{k}{x}$(x>0)上,它们的横坐标分别为a,(n+1)a,
∴点P1,Pn+1(n=1,2,…,2011)的纵坐标为$\frac{2}{a}$,$\frac{2}{(n+1)a}$,
如图,过P1、Pn+1分别作x轴、y轴的平行线,
可得Sn=S△P1Pn+1O=(n+1)a•$\frac{2}{a}$-$\frac{1}{2}$a•$\frac{2}{a}$-$\frac{1}{2}$(n+1)a•$\frac{2}{(n+1)a}$-$\frac{1}{2}$[(n+1)a-a][$\frac{2}{a}$-$\frac{2}{(n+1)a}$]=n+$\frac{n}{n+1}$,
由Q在双曲线y=$\frac{k}{x}$上,得到S=S△QMO=1,
则S1+S2+…+S2011+$\frac{S}{2}$+$\frac{S}{3}$+…+$\frac{S}{2012}$=(1+$\frac{1}{2}$)+(2+$\frac{2}{3}$)+…+(2011+$\frac{2011}{2012}$)=1+2+…+2011+1×2011=2025077.
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法求函数解析式,三角形面积求法,熟练掌握待定系数法是解本题的关键.

| A. | 2,3,5 | B. | 4,4,8 | C. | 14,6,7 | D. | 15,10,9 |
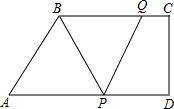 如图,在梯形ABCD中,∠D=90°,BC∥AD.BC=20,DC=16,AD=30,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
如图,在梯形ABCD中,∠D=90°,BC∥AD.BC=20,DC=16,AD=30,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)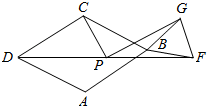 如图,菱形ABCD中,∠ABC=60°,BF=BG,∠GBF=60°,P是DF的中点,连接PG、PC.若∠CPD=60°,PG=$\frac{5\sqrt{3}}{2}$,DF=8,则菱形的边长为$\frac{7}{2}$.
如图,菱形ABCD中,∠ABC=60°,BF=BG,∠GBF=60°,P是DF的中点,连接PG、PC.若∠CPD=60°,PG=$\frac{5\sqrt{3}}{2}$,DF=8,则菱形的边长为$\frac{7}{2}$. 如图,长方形ABCD在坐标平面内,点A的坐标是A(2,1),且边AB、CD与x轴平行,边AD、BC与y轴平行,点B、C的坐标分别为B(a,1),C(a,c),且a、c满足关系式.c=$\sqrt{a-6}$+$\sqrt{6-a}$+3
如图,长方形ABCD在坐标平面内,点A的坐标是A(2,1),且边AB、CD与x轴平行,边AD、BC与y轴平行,点B、C的坐标分别为B(a,1),C(a,c),且a、c满足关系式.c=$\sqrt{a-6}$+$\sqrt{6-a}$+3