题目内容
2.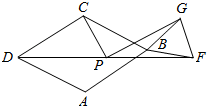 如图,菱形ABCD中,∠ABC=60°,BF=BG,∠GBF=60°,P是DF的中点,连接PG、PC.若∠CPD=60°,PG=$\frac{5\sqrt{3}}{2}$,DF=8,则菱形的边长为$\frac{7}{2}$.
如图,菱形ABCD中,∠ABC=60°,BF=BG,∠GBF=60°,P是DF的中点,连接PG、PC.若∠CPD=60°,PG=$\frac{5\sqrt{3}}{2}$,DF=8,则菱形的边长为$\frac{7}{2}$.
分析 延长GP交DA于点E,连接EC,GC,可证明△DPE≌△FPG,再证得△CDE≌△CBG,利用在Rt△CPG中由三角函数可求得PC,在Rt△PCD中,由勾股定理可求得DC,可得出答案.
解答 解:如图,延长GP交DA于点E,连接EC,GC,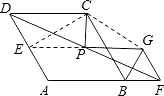
∵BF=BG,∠GBF=60°,
∴△BGF正三角形,
∵∠ABC=60°,
∴GF∥BC∥AD,
∴∠EDP=∠GFP,
在△DPE和△FPG中,
$\left\{\begin{array}{l}{∠EDP=∠GFP}\\{DP=FP}\\{∠DPE=∠FPG}\end{array}\right.$,
∴△DPE≌△FPG(ASA),
∴PE=PG,DE=FG=BG,
∵∠CDE=∠CBG=60°,CD=CB,
在△CDE和△CBG中,
$\left\{\begin{array}{l}{CD=CB}\\{∠CDE=∠CBE=60°}\\{DE=BG}\end{array}\right.$,
∴△CDE≌△CBG(SAS),
∴CE=CG,∠DCE=∠BCG,
∴∠ECG=∠DCB=120°,
∵PE=PG,
∴CP⊥PG,∠PCG=$\frac{1}{2}$∠ECG=60°,
∴PG=$\sqrt{3}$PC=$\frac{5\sqrt{3}}{2}$,
∴PC=$\frac{5}{2}$,
∵P为DF的中点,
∴DP=$\frac{1}{2}$DF=$\frac{1}{2}$×8=4,
在Rt△PCD中,CD=$\sqrt{D{P}^{2}-C{P}^{2}}=\sqrt{{4}^{2}-(\frac{5}{2})^{2}}=\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
点评 本题考查了菱形的性质、全等三角形的性质定理和判定定理、勾股定理的应用,解决本题的关键是作出辅助线,证明三角形全等.

| A. | 3x+1=4x-2 | B. | 3x-1=4x+2 | C. | $\frac{x-1}{3}$=$\frac{x+2}{4}$ | D. | $\frac{x+1}{3}$=$\frac{x-2}{4}$ |
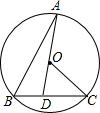 如图,BC是⊙O弦,D是BC上一点,DO交⊙O于点A,连接AB、OC,若∠A=20°,∠C=30°,则∠AOC的度数为100°.
如图,BC是⊙O弦,D是BC上一点,DO交⊙O于点A,连接AB、OC,若∠A=20°,∠C=30°,则∠AOC的度数为100°.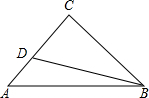 如图,已知:在△ABC中,∠C=90°,AC=BC,D为AC上一点,且tan∠ABD=$\frac{1}{5}$,求AD:DC的值.
如图,已知:在△ABC中,∠C=90°,AC=BC,D为AC上一点,且tan∠ABD=$\frac{1}{5}$,求AD:DC的值.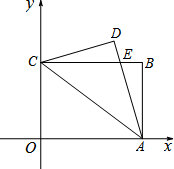 已知:如图,平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别为(4,0),(0,3).将△OCA沿直线CA翻折,得到△DCA,且DA交CB于点E.
已知:如图,平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别为(4,0),(0,3).将△OCA沿直线CA翻折,得到△DCA,且DA交CB于点E.