题目内容
6.解下列方程:(1)6x2+x=2;
(2)4x2-3x-2=0;
(3)3y2-y-5=0;
(4)5x=7x2-1.
分析 (1)先移项得到6x2+x-2=0,然后利用因式分解法解方程;
(2)(3)利用公式法解方程;
(4)先把方程化为一般式,然后利用公式法求解.
解答 解:(1)6x2+x-2=0,
(3x+2)(2x-1)=0,
3x+2=0或2x-1=0,
所以x1=-$\frac{2}{3}$,x2=$\frac{1}{2}$;
(2)△=(-3)2-4×4×(-2)=41,
x=$\frac{3±\sqrt{41}}{2×4}$,
所以x1=$\frac{3+\sqrt{41}}{8}$,x2=$\frac{3-\sqrt{41}}{8}$;
(3))△=(-1)2-4×3×(-5)=61,
y=$\frac{1±\sqrt{61}}{2×3}$,
所以y1=$\frac{1+\sqrt{61}}{6}$,y2=$\frac{1-\sqrt{61}}{6}$;
(4)7x2-5x-1=0,
△=(-5)2-4×7×(-1)=53,
x=$\frac{5±\sqrt{53}}{2×7}$,
所以x1=$\frac{5+\sqrt{53}}{14}$,x2=$\frac{5-\sqrt{53}}{14}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了公式法解一元二次方程.

练习册系列答案
相关题目
11.七年级(1)班给几位三好学生发笔记本作为奖品,若每位三好学生发3本,则剩下1本,若每位三好学生发4本,则少2本,问笔记本共有几本?若设共有x本笔记本,则列出的方程是( )
| A. | 3x+1=4x-2 | B. | 3x-1=4x+2 | C. | $\frac{x-1}{3}$=$\frac{x+2}{4}$ | D. | $\frac{x+1}{3}$=$\frac{x-2}{4}$ |
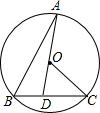 如图,BC是⊙O弦,D是BC上一点,DO交⊙O于点A,连接AB、OC,若∠A=20°,∠C=30°,则∠AOC的度数为100°.
如图,BC是⊙O弦,D是BC上一点,DO交⊙O于点A,连接AB、OC,若∠A=20°,∠C=30°,则∠AOC的度数为100°.
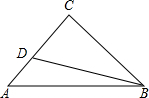 如图,已知:在△ABC中,∠C=90°,AC=BC,D为AC上一点,且tan∠ABD=$\frac{1}{5}$,求AD:DC的值.
如图,已知:在△ABC中,∠C=90°,AC=BC,D为AC上一点,且tan∠ABD=$\frac{1}{5}$,求AD:DC的值.