题目内容
5.如图(1),在平面直角坐标系中.以坐标原点O为圆心的⊙O的半径为$\sqrt{2}$-1,直线l:y=x-$\sqrt{2}$与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与x轴相切于M(1)求A的坐标及∠CAO的度数;
(2)⊙B以每秒1个单位长度沿x轴正方向平移,同时直线l绕点A逆时针匀速旋转,当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切,问直线AC绕点A每秒旋转多少度?
(3)如图(2)过A、O、C三点作⊙O1,点E是劣弧AO上一点,连接EC、EA、ED,当点E在劣弧AO上运动时(E不与A、O两点重合),则$\frac{EC-EA}{EO}$的值是否发生变化?如果不变,求其值:如果变化,说明理由
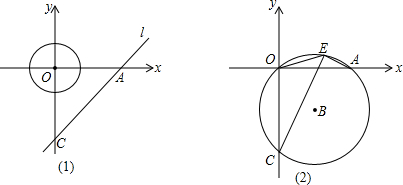
分析 (1)由直线l的方程可求得A、C的坐标,在Rt△AOC中可求得∠CAO的度数;
(2)如图,设⊙B平移t秒到⊙B1处与⊙O第一次相切,直线l旋转到l1恰好与⊙B1第一次相切于点P,⊙B1与x轴相切于点N,连接B1O,B1N.由相切可求得OB1,可求得t的值,连接B1A,B1P,可证得PA∥B1O,则可求得∠1=90°,可求得直线l旋转的角度;
(3)由(1)可知AC为⊙O1的直径,在CE截取CM,使CM=AE,OA=OC,再由同弧所对的圆周角相等得到一对角相等,利用SAS得到三角形AOE与三角形COM全等,由全等三角形的对应角相等得到一对角相等,利用同角的余角相等得到∠EOM为直角,对应边相等得到OE=OM,可得出三角形EOM为等腰直角三角形,利用勾股定理得到EM=$\sqrt{2}$OE,再由EM=EC-CM,等量代换即可求出所求式子的结果.
解答 解:(1)在y=x-$\sqrt{2}$中,令y=0可得x=$\sqrt{2}$,令x=0,可得y=-$\sqrt{2}$,
∴A($\sqrt{2}$,0),C(0,-$\sqrt{2}$),
∴OA=OC=$\sqrt{2}$,
∴∠CAO=45°;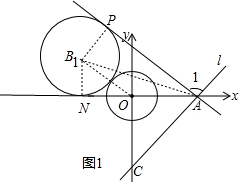 (2)如图1,设⊙B平移t秒到⊙B1处与⊙O第一次相切,
(2)如图1,设⊙B平移t秒到⊙B1处与⊙O第一次相切,
此时,直线l旋转到l1恰好与⊙B1第一次相切于点P,⊙B1与x轴相切于点N,连接B1O,B1N.
则MN=t,OB1=$\sqrt{2}$,B1N=1,B1N⊥AN.
∴ON=1,
∴MN=3,即t=3.
连接B1A,B1P,则B1P⊥AP,B1P=B1N,
∴∠PAB1=∠NAB1.
∵OA=OB1=$\sqrt{2}$,
∴∠AB1O=∠NAB1.
∴∠PAB1=∠AB1O.
∴PA∥B1O.
在Rt△NOB1中,∠B1ON=45°,
∴∠PAN=45°,
∴∠1=90°.
∴直线AC绕点A平均每秒旋转90°÷3=30°;
(3)解:如图2,由(1)可知△OAC为⊙O1的内接等腰直角三角形,AC为直径,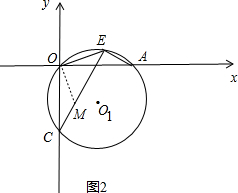 在CE上截取CM=AE,连接OM,
在CE上截取CM=AE,连接OM,
∵在△OAE和△OCM中,
$\left\{\begin{array}{l}{OA=OC}\\{∠OAE=∠OCM}\\{AE=CM}\end{array}\right.$,
∴△OAE≌△OCM(SAS),
∴∠AOE=∠COM,OM=OE,
∵∠AOC=∠AOM+∠MOC=90°,∠MOE=∠AOE+∠AOM,
∴∠MOE=90°,
∴△OME为等腰直角三角形,
∴ME=$\sqrt{2}$EO,
又∵ME=EC-CM=EC-AE,
∴EC-AE=$\sqrt{2}$EO,即$\frac{EC-EA}{EO}$=$\sqrt{2}$,
∴当点E在劣弧AO上运动时(E不与A、O两点重合),则$\frac{EC-EA}{EO}$的值不变,其值为$\sqrt{2}$.
点评 本题主要考查圆的综合应用,涉及圆和圆的相切、直线和圆相切的性质、全等三角形的判定和性质、等腰直角三角形的性质等知识.在(1)中注意等腰直角三角形的性质,在(2)中先求得t的值是解题的关键,在(3)中构造三角形全等,找到ME和EO的关系是解题的关键.本题涉及知识点较多,综合性很强,有一定的难度.

| A. | 相等 | B. | 互相垂直 | C. | 相等且互相垂直 | D. | 相等且互相平分 |
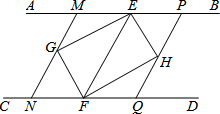 如图,AB∥CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
如图,AB∥CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H. 如图,已知:在△ABC中,∠C=90°,AC=BC,D为AC上一点,且tan∠ABD=$\frac{1}{5}$,求AD:DC的值.
如图,已知:在△ABC中,∠C=90°,AC=BC,D为AC上一点,且tan∠ABD=$\frac{1}{5}$,求AD:DC的值.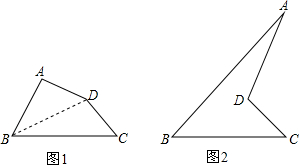
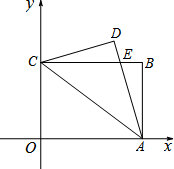 已知:如图,平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别为(4,0),(0,3).将△OCA沿直线CA翻折,得到△DCA,且DA交CB于点E.
已知:如图,平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别为(4,0),(0,3).将△OCA沿直线CA翻折,得到△DCA,且DA交CB于点E.