题目内容
16．如图1，已知A、B、C三点的坐标分别为A（1，0），B（4，0），C（5，5）．试在给出的直角坐标平面内画△ABC，再画△A′B′C′，使得△A′B′C′≌△ABC，并求出△A′B′C′的面积．
分析 先描点画出△ABC，再写出A、B、C点关于y轴的对称点A′、B′、C′的坐标，描点即可得到△A′B′C′，则△A′B′C′≌△ABC，然后利用三角形面积公式计算△A′B′C′的面积．
解答 解：如图，△ABC和△A′B′C′为所画，△A′B′C′的面积=$\frac{1}{2}$×3×5=$\frac{15}{2}$．
点评 本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
练习册系列答案
相关题目
如图，反比例函数y=$\frac{6}{x}$（x＞0）的图象和矩形ABCD都在第一象限内，AD与x轴平行，已知点A的坐标是（2，6），AB=2，AD=4．现将矩形ABCD向下平移m个单位，要使矩形ABCD与反比例函数y=$\frac{6}{x}$（x＞0）的图象有交点，则m的取值范围是1≤m≤5．
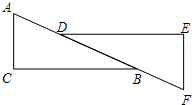如图，在△ABC与△FDE中，点D在AB上，点B在DF上，∠C=∠E，AC∥FE，AD=FB．求证：△ABC≌△FDE．
已知正六边形的边长为4cm，分别以它的三个不相邻的顶点为圆心，边长为半径画弧（如图），则所得到的三条弧的长度之和为8πcm．（结果保留π）
如图1，已知GF∥BC．
如图，在△ABC中，BD是∠ABC的平分线，CD是∠ACE的平分线，试探索∠D与∠A的数量关系，并说明理由．
如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长交BC于点G．连接AG．求证：△ABG≌△AFG．
如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=$\frac{BC}{CD}$；②S△ABC+S△CDE≥S△ACE；③BM⊥DM；④BM=DM．正确结论的序号是①②③④．