题目内容
6. 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=$\frac{BC}{CD}$;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的序号是①②③④.
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=$\frac{BC}{CD}$;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的序号是①②③④.
分析 ①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知$\frac{AC}{EC}$=$\frac{AB}{ED}$=$\frac{BC}{CD}$;然后由直角三角形中的正切函数,得tan∠AEC=$\frac{AC}{EC}$,再由等量代换求得tan∠AEC=$\frac{BC}{CD}$;
②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab(a=b时取等号)解答;
③④通过作辅助线MN,构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答.
解答  解:∵△ABC和△CDE均为等腰直角三角形,
解:∵△ABC和△CDE均为等腰直角三角形,
∴AB=BC,CD=DE,
∴∠BAC=∠BCA=∠DCE=∠DEC=45°,
∴∠ACE=90°;
∵△ABC∽△CDE
∴$\frac{AC}{EC}$=$\frac{AB}{ED}$=$\frac{BC}{CD}$①∴tan∠AEC=$\frac{AC}{EC}$,
∴tan∠AEC=$\frac{BC}{CD}$;故本选项正确;
②∵S△ABC=$\frac{1}{2}$a2,S△CDE=$\frac{1}{2}$b2,S梯形ABDE=$\frac{1}{2}$(a+b)2,
∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab,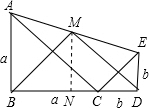 S△ABC+S△CDE=$\frac{1}{2}$(a2+b2)≥ab(a=b时取等号),
S△ABC+S△CDE=$\frac{1}{2}$(a2+b2)≥ab(a=b时取等号),
∴S△ABC+S△CDE≥S△ACE;故本选项正确;
④过点M作MN垂直于BD,垂足为N.
∵点M是AE的中点,
则MN为梯形中位线,
∴N为中点,
∴△BMD为等腰三角形,
∴BM=DM;故本选项正确;
③又MN=$\frac{1}{2}$(AB+ED)=$\frac{1}{2}$(BC+CD),
∴∠BMD=90°,
即BM⊥DM;故本选项正确.
故答案为:①②③④.
点评 本题考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点.注意准确作出辅助线是解此题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
| A. | 3$\sqrt{\frac{2}{3}}$=$\sqrt{2}$ | B. | -3$\sqrt{2}$=$\sqrt{(-3)^{2}×2}$ | C. | $\sqrt{(-2)^{6}}$=(-2)3 | D. | $\sqrt{(a-b)^{4}}$=(a-b)2 |
| A. | 6a-5a=1 | B. | a2+a2=2a4 | C. | 3a2b-4b2a=-a2b | D. | 2a3+3a3=5a3 |
 如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD=∠C=45°,AB=8,CD=9,则AD的长为5.
如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD=∠C=45°,AB=8,CD=9,则AD的长为5.
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1.给出四个结论:①b2>4ac;②b=-2a;③a+b+c=0;④c-a>0,其中正确结论的番号是①④.
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1.给出四个结论:①b2>4ac;②b=-2a;③a+b+c=0;④c-a>0,其中正确结论的番号是①④.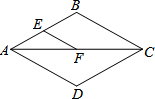 如图,AC是菱形ABCD的对角线,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是16.
如图,AC是菱形ABCD的对角线,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是16.