题目内容
1. 如图1,已知GF∥BC.
如图1,已知GF∥BC.(1)试说明:∠F+∠C=∠FAC;
(2)如图2,若AQ平分∠FAC,交BC于Q,且∠Q=15°,∠F=50°,求∠ACB的度数.
分析 (1)作EF∥AB,如图,由于GF∥BC,则AE∥GF,于是根据平行线的性质得∠1=∠F,∠2=∠C,所以有∠FAC=∠1+∠2=∠F+∠C.
(2)根据三角形外角的性质得∠ACB=$\frac{1}{2}$∠FAC+∠Q,由(1)可知∠FAC=∠F+∠ACB,代入计算即可求得.
解答 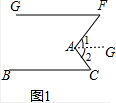 解:(1)作AE∥BC,如图1,
解:(1)作AE∥BC,如图1,
∵GF∥BC,
∴AE∥GF,
∴∠1=∠F,∠2=∠C,
∴∠1+∠2=∠F+∠C,
即∠F+∠C=∠FAC;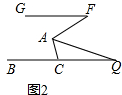
(2)如图2,由(1)可知∠FAC=∠F+∠ACB,
∵∠ACB=$\frac{1}{2}$∠FAC+∠Q,
∴∠ACB=$\frac{1}{2}$(∠F+∠ACB)+∠Q,
∴∠ACB=∠F+2∠Q=50°+30°=80°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
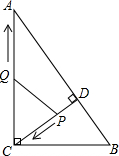 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒. 如图,点A、B分别表示的数是6、-12,M、N、P为数轴上三个动点,它们同时都向右运动.点M从点A出发,速度为每秒2个单位长度,点N从点B出发,速度为点M的3倍,点P从原点出发,速度为每秒1个单位长度.
如图,点A、B分别表示的数是6、-12,M、N、P为数轴上三个动点,它们同时都向右运动.点M从点A出发,速度为每秒2个单位长度,点N从点B出发,速度为点M的3倍,点P从原点出发,速度为每秒1个单位长度. 如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y=10.
如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y=10.
 如图所示,已知∠ACB=90°,∠ADC=90°,图中互相垂直的线段有AC⊥BC,CD⊥AB.
如图所示,已知∠ACB=90°,∠ADC=90°,图中互相垂直的线段有AC⊥BC,CD⊥AB. 如图,∠A=50°,∠DCB=100°,CE是∠DCB的平分线,CE∥AB吗?为什么?
如图,∠A=50°,∠DCB=100°,CE是∠DCB的平分线,CE∥AB吗?为什么?