题目内容
6. 如图,反比例函数y=$\frac{6}{x}$(x>0)的图象和矩形ABCD都在第一象限内,AD与x轴平行,已知点A的坐标是(2,6),AB=2,AD=4.现将矩形ABCD向下平移m个单位,要使矩形ABCD与反比例函数y=$\frac{6}{x}$(x>0)的图象有交点,则m的取值范围是1≤m≤5.
如图,反比例函数y=$\frac{6}{x}$(x>0)的图象和矩形ABCD都在第一象限内,AD与x轴平行,已知点A的坐标是(2,6),AB=2,AD=4.现将矩形ABCD向下平移m个单位,要使矩形ABCD与反比例函数y=$\frac{6}{x}$(x>0)的图象有交点,则m的取值范围是1≤m≤5.
分析 根据矩形性质得出AB=CD=2,AD=BC=4,即可得出B(2,4),C(6,4),D(6,6),根据向下平移横坐标不变,分别代入B的横坐标和D的横坐标求得对应的函数值,即可求得m的取值范围.
解答 解:∵四边形ABCD是矩形,平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
∴AB=CD=2,AD=BC=4,
∴B(2,4),C(6,4),D(6,6);
当B点落在反比例函数的图象上时,把x=2代入y=$\frac{6}{x}$得,y=3,
∴m=4-3=1,
当D点落在反比例函数的图象上时,把x=6代入y=$\frac{6}{x}$得,y=1,
∴m=6-1=5,
∴要使矩形ABCD与反比例函数y=$\frac{6}{x}$(x>0)的图象有交点,则m的取值范围是1≤m≤5.
故答案为1≤m≤5.
点评 本题考查了矩形性质和反比例函数图象上点的坐标特征,平移的性质的应用,求得B、D的坐标是解题的关键.

练习册系列答案
相关题目
14. 如图,在△ABC中,AB=AC,∠A=25°,DE垂直平分AC,交AB于点D,连接CD,则∠BCD的度数为( )
如图,在△ABC中,AB=AC,∠A=25°,DE垂直平分AC,交AB于点D,连接CD,则∠BCD的度数为( )
 如图,在△ABC中,AB=AC,∠A=25°,DE垂直平分AC,交AB于点D,连接CD,则∠BCD的度数为( )
如图,在△ABC中,AB=AC,∠A=25°,DE垂直平分AC,交AB于点D,连接CD,则∠BCD的度数为( )| A. | 50° | B. | 25° | C. | 52.5° | D. | 无法确定 |
 如图,AB∥EF,∠C=∠D=85°,CF=BD,若∠A=40°,则∠EFD=55°.
如图,AB∥EF,∠C=∠D=85°,CF=BD,若∠A=40°,则∠EFD=55°. 如图,在△ABC中,∠BAC=90°,D、E、F分别为边AB、BC、AC的中点,若AE=5,则DF=5.
如图,在△ABC中,∠BAC=90°,D、E、F分别为边AB、BC、AC的中点,若AE=5,则DF=5.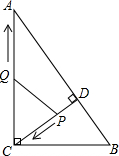 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒.