题目内容
8.结合数轴与绝对值的知识回答下列问题: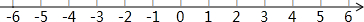
(1)数轴上表示4和1的两点之间的距离是3;表示-3和2两点之间的距离是5;一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|.如果表示数a和-2的两点之间的距离是3,那么a=-5或1
(2)若数a表示数轴上的整数点,当a取何值时,|a+1|+|a-2|的值最小,最小为多少?
分析 (1)根据数轴,观察两点之间的距离即可解决;
(2)根据|a+1|+|a-2|表示数a的点到-1与2两点的距离的和即可求解.
解答 解:(1)数轴上表示4和1的两点之间的距离是4-1=3;
表示-3和2两点之间的距离是2-(-3)=5;
如果表示数a和-2的两点之间的距离是3,那么a=1或-5;
(2)若数轴上表示数a的点位于-1与2之间,
|a+1|+|a-2|=(a+1)+(2-a)=3.
故答案为3,5,-5或1.
点评 本题考查数轴上两点之间的距离的算法:数轴上两点之间的距离等于相应两数差的绝对值,应牢记且会灵活应用.

练习册系列答案
相关题目
18.某企业2014年的生产总值为a万元,预计2015年的生产总值比去年增长20%,那么该企业这两年的生产总值之和是( )
| A. | 20%a万元 | B. | (20%+a)万元 | C. | (1+20%)a万元 | D. | [a+(1+20%)a]万元 |
19.下列说法中正确的是( )
| A. | 带根号的数都是无理数 | B. | 无限小数都是无理数 | ||
| C. | 无理数都是无限小数 | D. | 两个无理数的和一定是无理数 |
16.对于函数y=-$\frac{5}{x}$,下列说法错误的是( )
| A. | 它的图象分布在二、四象限 | |
| B. | 它的图象既是轴对称图形又是中心对称图形 | |
| C. | 当x>0时,y的值随x的增大而增大 | |
| D. | 当x<0时,y的值随x的增大而减小 |
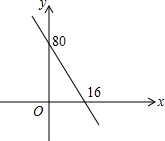 某汽车销售公司销售某种型号的汽车,每辆车进价6万元,售价为x万元,经市场调查发现销售量y与销售价x的关系如图.
某汽车销售公司销售某种型号的汽车,每辆车进价6万元,售价为x万元,经市场调查发现销售量y与销售价x的关系如图.