题目内容
16．对于函数y=-$\frac{5}{x}$，下列说法错误的是（ ）| A． | 它的图象分布在二、四象限 | |
| B． | 它的图象既是轴对称图形又是中心对称图形 | |
| C． | 当x＞0时，y的值随x的增大而增大 | |
| D． | 当x＜0时，y的值随x的增大而减小 |
分析 根据反比例函数y=$\frac{k}{x}$的性质：当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大，图象既是轴对称图形又是中心对称图形进行判断即可．
解答 解：A、它的图象分布在二、四象限，说法正确；
B、它的图象既是轴对称图形又是中心对称图形，说法正确；
C、当x＞0时，y的值随x的增大而增大，说法正确；
D、当x＜0时，y的值随x的增大而减小，说法错误；
故选：D．
点评 此题主要考查了反比例函数的性质，关键是掌握反比例函数y=$\frac{k}{x}$的性质：
（1）反比例函数y=xk（k≠0）的图象是双曲线；
（2）当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小；
（3）当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大．
注意：反比例函数的图象与坐标轴没有交点．
练习册系列答案
相关题目
6．（1）计算：（-$\frac{1}{2}$+$\frac{2}{3}$-$\frac{1}{4}$）×|-24|
（2）计算：-13-（1-0.5）×$\frac{1}{3}$×[2-（-3）2]．
（2）计算：-13-（1-0.5）×$\frac{1}{3}$×[2-（-3）2]．
11．矩形具有而菱形不一定具有的性质是（ ）
| A． | 对角线互相平分 | B． | 对角线相等 | C． | 四条边都相等 | D． | 对角线互相垂直 |
5．对于两个实数a，b，用max（a，b）表示其中较大的数，则方程x×max（x，-x）=2x+1的解是（ ）
| A． | 1，1+$\sqrt{2}$ | B． | 1，1-$\sqrt{2}$ | C． | -1，1+$\sqrt{2}$ | D． | -1，1-$\sqrt{2}$ |
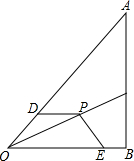如图，点P为OC上一点，PD=PE，∠0DP+∠OEP=180°，求证：0P平分∠A0B．