题目内容
3.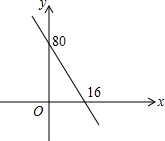 某汽车销售公司销售某种型号的汽车,每辆车进价6万元,售价为x万元,经市场调查发现销售量y与销售价x的关系如图.
某汽车销售公司销售某种型号的汽车,每辆车进价6万元,售价为x万元,经市场调查发现销售量y与销售价x的关系如图.(1)请求出销售利润W与销售价x的关系式,并求出销售价x为多少时,利润W最大,最大值是多少?
(2)今年12月份销售价为10万元,12月中旬由于油价上涨等诸多因素,可能明年将影响到销售量,公司做了全面的调查研究发现:同时把销售价下调a%,销售量就会比不降价时提高3a%.结果利润仍然有114万元,请确定a的值.(精确到0.01)(注:$\sqrt{6}=2.449$$\sqrt{7}=2.646$$\sqrt{8}=2.829$)
分析 (1)由图可知销售量y与销售价x是一次函数,设出函数解析式,求得y与x之间的关系式,进一步利用销售利润=每一辆的销售利润×销售量得出销售利润W与销售价x的关系式,利用二次函数的性质求得最大值即可;
(2)利用用销售利润=每一辆的销售利润×销售量得出关于a的一元二次方程,求得方程的解,确定a的数值即可.
解答 解:(1)由图知y是x的一次函数,设y=kx+b,
由图知$\left\{\begin{array}{l}16k+b=0\\ b=80\end{array}\right.$,
解得:$\left\{\begin{array}{l}k=-5\\ b=80\end{array}\right.$.
因此y=-5x+80,
则销售利润W与销售价x的关系式:W=(x-6)(-5x+80)=-5x2+110x-480;
∵W=-5x2+110x-480=-5(x-11)2+125,-5<0,
∴x=11时,W最大=125,
即销售价x为11万元时,利润W最大,最大值125万元.
(2)由(1)知y=-5x+80,
当x=10时,y=30,
由题意得:[10(1-a%)-6]×30(1+3a%)=114,
解得:a1=$\frac{{20-20\sqrt{7}}}{6}$<0(不符合题意,舍去),a2=$\frac{{20+20\sqrt{7}}}{6}$≈12.15.
答:确定a的值是12.15.
点评 此题考查二次函数的实际运用,一元二次方程的实际运用,待定系数法求函数解析式,掌握销售问题中的基本数量关系是解决问题的关键.

练习册系列答案
相关题目
11.矩形具有而菱形不一定具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线相等 | C. | 四条边都相等 | D. | 对角线互相垂直 |
15.迄今为止,科学家发现了约76万种昆虫,这张表表示昆虫的主要类群种数.利用这些数据,绘制一张扇形图,来表示每种昆虫所占的百分比.
| 种群 | 蚂蚁、蜜蜂和黄蜂 | 甲虫、象鼻虫 | 蝴蝶、蛾 | 苍蝇、蚊子 | 其他昆虫 |
| 种数/万 | 10 | 30 | 11 | 10 | 15 |
12.m条直线两两相交,最多有10个交点,则列得的方程是( )
| A. | 2m=10 | B. | m+(m-1)=10 | C. | $\frac{m(m-1)}{2}$=10 | D. | m(m-1)=10 |
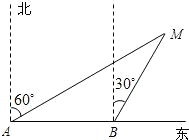 某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时40海里的速度向正东方向航行,1小时后到达B处,在B处观测到灯塔M在北偏东30°方向处.则B处与灯塔的距离BM是40海里.
某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时40海里的速度向正东方向航行,1小时后到达B处,在B处观测到灯塔M在北偏东30°方向处.则B处与灯塔的距离BM是40海里.
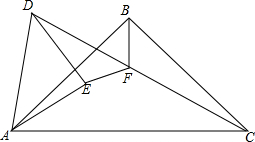 如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由.
如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由.