题目内容
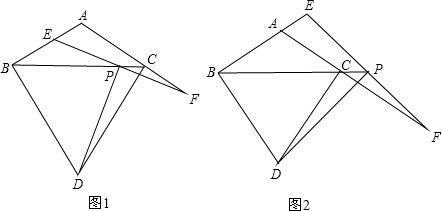
16.如图1,△ABC中,AB=AC,连B,C分别作BD⊥AB,CD⊥AC,BD、CD相交于D点,P为BC上一点,过P的直线交AB于E,AC延长线于F,且满足PE=PF,连结DP.(1)求证:DP⊥EF;
(2)如图2,若P为BC延长线上,其它条件不变,(1)中结论是否成立?
分析 (1)连接AD,由HL证明Rt△ABD≌Rt△ACD,得出BD=CD,作EK∥AC交BC于K,连接DE、DF,则∠ACB=∠EKB,∠PCF=∠PKE,∠PFC=∠PEK,由AAS证明△PCF≌△PKE,得出CF=KE,由等腰三角形的性质证出∠EKB=∠ABC,得出BE=KE=CF,由SAS证明△BDE≌△CDF,得出DE=DF,由等腰三角形的性质即可得出结论;
(2)连接AD,由HL证明Rt△ABD≌Rt△ACD,得出BD=CD,作EK∥AC交BC的延长线于K,连接DE、DF,则∠ACB=∠EKB,∠PCF=∠PKE,∠PFC=∠PEK,由AAS证明△PCF≌△PKE,得出CF=KE,由等腰三角形的性质证出∠EKB=∠ABC,得出BE=KE=CF,由SAS证明△BDE≌△CDF,得出DE=DF,由等腰三角形的性质即可得出结论;
解答 (1)证明:连接AD,如图1所示: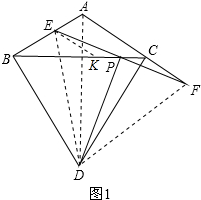
∵BD⊥AB,CD⊥AC,
∴∠ABD=∠ACD=∠DCF=90°,
在Rt△ABD和Rt△ACD中,$\left\{\begin{array}{l}{AD=AD}\\{AB=AC}\end{array}\right.$,
∴Rt△ABD≌Rt△ACD(HL),
∴BD=CD,作EK∥AC交BC于K,连接DE、DF,
则∠ACB=∠EKB,∠PCF=∠PKE,∠PFC=∠PEK,
在△PCF和△PKE中,$\left\{\begin{array}{l}{∠PCF=∠PKE}&{\;}\\{∠PFC=∠PEK}&{\;}\\{PF=PE}&{\;}\end{array}\right.$,
∴△PCF≌△PKE(AAS),
∴CF=KE,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠EKB=∠ABC,
∴BE=KE=CF,
在△BDE和△CDF中,$\left\{\begin{array}{l}{BE=CF}&{\;}\\{∠DBE=∠DCF}&{\;}\\{BD=CD}&{\;}\end{array}\right.$,
∴△BDE≌△CDF(SAS),
∴DE=DF,
∵PE=PF,
∴DP⊥EF;
(2)解:(1)中结论成立;理由如下:
连接AD,如图2所示: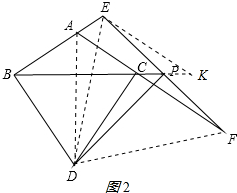
∵BD⊥AB,CD⊥AC,
∴∠ABD=∠ACD=∠DCF=90°,
在Rt△ABD和Rt△ACD中,$\left\{\begin{array}{l}{AD=AD}\\{AB=AC}\end{array}\right.$,
∴Rt△ABD≌Rt△ACD(HL),
∴BD=CD,
作EK∥AC交BC的延长线于K,连接DE、DF,
则∠ACB=∠EKB,∠PCF=∠PKE,∠PFC=∠PEK,
在△PCF和△PKE中,$\left\{\begin{array}{l}{∠PCF=∠PKE}&{\;}\\{∠PFC=∠PEK}&{\;}\\{PF=PE}&{\;}\end{array}\right.$,
∴△PCF≌△PKE(AAS),
∴CF=KE,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠EKB=∠ABC,
∴BE=KE=CF,
在△BDE和△CDF中,$\left\{\begin{array}{l}{BE=CF}&{\;}\\{∠DBE=∠DCF}&{\;}\\{BD=CD}&{\;}\end{array}\right.$,
∴△BDE≌△CDF(SAS),
∴DE=DF,
∵PE=PF,
∴DP⊥EF;
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、平行线的性质等知识;本题综合性强,难度较大,需要通过作辅助线多次证明三角形全等才能得出结论.

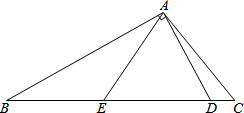 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.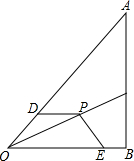 如图,点P为OC上一点,PD=PE,∠0DP+∠OEP=180°,求证:0P平分∠A0B.
如图,点P为OC上一点,PD=PE,∠0DP+∠OEP=180°,求证:0P平分∠A0B.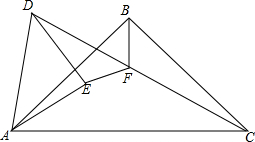 如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由.
如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由.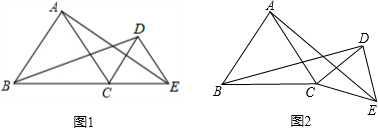
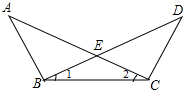 已知:如图,∠A=∠D,∠1=∠2,你能证明图中哪些线段相等?哪些角相等?
已知:如图,∠A=∠D,∠1=∠2,你能证明图中哪些线段相等?哪些角相等?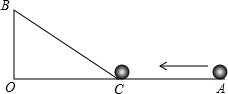 如图,∠AOB=90°,OA=25m,OB=5m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=25m,OB=5m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?