题目内容
20.在△ABC中,∠C=90°,AB=3$\sqrt{6}$,BC=3$\sqrt{3}$,解这个直角三角形.分析 首先根据勾股定理推出AC的长度,然后根据AC和AB的关系即可推出∠B的度数,进而求出∠A的度数.
解答 解:∵∠C=90°,AB=3$\sqrt{6}$,BC=3$\sqrt{3}$,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{(3\sqrt{6})^{2}-(3\sqrt{3})^{2}}$=3$\sqrt{3}$,
∴sinB=$\frac{AC}{AB}$=$\frac{3\sqrt{3}}{3\sqrt{6}}$=$\frac{\sqrt{2}}{2}$,
∴∠B=45°,
∴∠A=90°-∠B=45°.
点评 本题主要考查勾股定理,角的三角函数值,关键在于推出AC的长度,认真的进行计算,熟练掌握特殊角的三角函数值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.矩形具有而菱形不一定具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线相等 | C. | 四条边都相等 | D. | 对角线互相垂直 |
15.迄今为止,科学家发现了约76万种昆虫,这张表表示昆虫的主要类群种数.利用这些数据,绘制一张扇形图,来表示每种昆虫所占的百分比.
| 种群 | 蚂蚁、蜜蜂和黄蜂 | 甲虫、象鼻虫 | 蝴蝶、蛾 | 苍蝇、蚊子 | 其他昆虫 |
| 种数/万 | 10 | 30 | 11 | 10 | 15 |
5.对于两个实数a,b,用max(a,b)表示其中较大的数,则方程x×max(x,-x)=2x+1的解是( )
| A. | 1,1+$\sqrt{2}$ | B. | 1,1-$\sqrt{2}$ | C. | -1,1+$\sqrt{2}$ | D. | -1,1-$\sqrt{2}$ |
12.m条直线两两相交,最多有10个交点,则列得的方程是( )
| A. | 2m=10 | B. | m+(m-1)=10 | C. | $\frac{m(m-1)}{2}$=10 | D. | m(m-1)=10 |
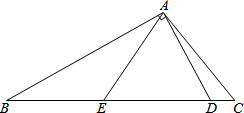 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.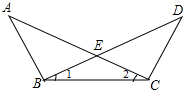 已知:如图,∠A=∠D,∠1=∠2,你能证明图中哪些线段相等?哪些角相等?
已知:如图,∠A=∠D,∠1=∠2,你能证明图中哪些线段相等?哪些角相等?