题目内容
 如图,将一幅宽20cm,长30cm的图案进行装裱,装裱后的整幅画长与宽的比与原画的长宽比相同,四周装裱的面积是原图案面积的
如图,将一幅宽20cm,长30cm的图案进行装裱,装裱后的整幅画长与宽的比与原画的长宽比相同,四周装裱的面积是原图案面积的| 11 |
| 25 |
考点:一元二次方程的应用
专题:几何图形问题
分析:由题意知长:宽=3:2,因装裱后的整幅画长与宽的比与原画的长宽比相同,故上下边衬和左右边衬的比例也为2:3,再利用四周装裱的面积是原图案面积的
找到等量关系,列出方程即可求得边衬的宽度.
| 11 |
| 25 |
解答:解:由题意知长:宽=3:2,因装裱后的整幅画长与宽的比与原画的长宽比相同,故上下边衬和左右边衬的比例也为3:2,
所以可设上下边衬的宽度为3xcm,左右边衬的宽度为2xcm,
则装裱后的面积为:(20+4x)(30+6x),且原面积为:30×20,
所以四周装裱的面积为:(20+4x)(30+6x)-30×20,
根据题意列方程:(20+4x)(30+6x)-30×20=
×30×20
整理得:x2+5x-11=0,
解得:x1=-11(舍去),x2=1,
所以上下边衬为3cm,左右边衬为2cm,
答:应按上下边衬为3cm,左右边衬为2cm来进行设计.
所以可设上下边衬的宽度为3xcm,左右边衬的宽度为2xcm,
则装裱后的面积为:(20+4x)(30+6x),且原面积为:30×20,
所以四周装裱的面积为:(20+4x)(30+6x)-30×20,
根据题意列方程:(20+4x)(30+6x)-30×20=
| 11 |
| 25 |
整理得:x2+5x-11=0,
解得:x1=-11(舍去),x2=1,
所以上下边衬为3cm,左右边衬为2cm,
答:应按上下边衬为3cm,左右边衬为2cm来进行设计.
点评:本题主要考查一元二次方程的应用,解题的关键是由题目条件得出上下边衬和左右边衬的比例.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

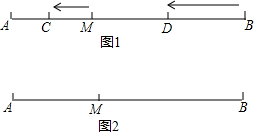 已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上).
已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上).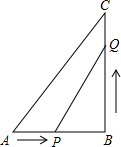 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始向B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P、Q分别从点A,B同时出发,经过多长时间△PBQ的面积等于6cm2?
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始向B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P、Q分别从点A,B同时出发,经过多长时间△PBQ的面积等于6cm2? 如图,A,B,C为圆O上的三等分点.
如图,A,B,C为圆O上的三等分点.