题目内容
13. 如图,AB∥CD,∠1=60°,则∠2=120°.
如图,AB∥CD,∠1=60°,则∠2=120°.
分析 先根据平行线的性质,得到∠CEF的度数,再根据邻补角的定义进行计算即可.
解答 解:∵AB∥CD,∠1=60°,
∴∠CEF=∠1=60°,
∴∠2=180°-∠CEF=120°,
故答案为:120°.
点评 本题主要考查了平行线的性质的运用,解题时注意:两直线平行,内错角相等.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
4. 如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
 如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
18.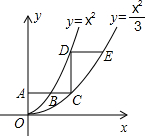 如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )
如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )
 如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )
如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )| A. | 2 | B. | y=$\frac{3}{2}$ | C. | 3-$\sqrt{2}$ | D. | 3-$\sqrt{3}$ |
2.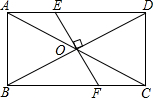 如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2$\sqrt{3}$,∠AEO=120°,则FC的长度为( )
如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2$\sqrt{3}$,∠AEO=120°,则FC的长度为( )
 如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2$\sqrt{3}$,∠AEO=120°,则FC的长度为( )
如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2$\sqrt{3}$,∠AEO=120°,则FC的长度为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 如图,点C是AB的中点,AD=CE,CD=BE.
如图,点C是AB的中点,AD=CE,CD=BE.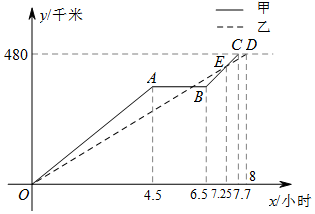 重阳节期间,某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游,由于人数较多,共租用甲、乙两辆长途汽车沿同一路线赶赴景点.图中的折线、线段分别表示甲、乙两车所走的路程y甲(千米),y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
重阳节期间,某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游,由于人数较多,共租用甲、乙两辆长途汽车沿同一路线赶赴景点.图中的折线、线段分别表示甲、乙两车所走的路程y甲(千米),y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题: 如图,在平面直角坐标系中有等腰Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(n,2).
如图,在平面直角坐标系中有等腰Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(n,2).