题目内容
5．解不等式组$\left\{\begin{array}{l}{2-x＞0}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}}\end{array}\right.$，并写出不等式组的整数解．分析 先求出不等式组的解集，再求出不等式组的整数解即可．
解答 解：$\left\{\begin{array}{l}{2-x＞0①}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}②}\end{array}\right.$
∵解不等式①得：x＜2，
解不等式②得：x≥-1，
∴不等式组的解集为-1≤x＜2，
∴不等式组的整数解为-1，0，1．
点评 本题考查了解一元一次不等式组，不等式组的整数解，能求出不等式组的解集是解此题的关键．
练习册系列答案
相关题目
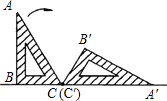如图，一块含有30°角的直角三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置，若BC=12cm，则顶点A从开始到结束所经过的路径长为16πcm．
如图，AB∥CD，∠1=60°，则∠2=120°．
如图所示，AB∥CD，EC⊥CD．若∠BEC=30°，则∠ABE的度数为120°．
15．下列实数，介于5和6之间的是（ ）
| A． | $\sqrt{21}$ | B． | $\sqrt{35}$ | C． | $\sqrt{42}$ | D． | $\root{3}{64}$ |