题目内容
15. 如图,点C是AB的中点,AD=CE,CD=BE.
如图,点C是AB的中点,AD=CE,CD=BE.(1)求证:△ACD≌△CBE;
(2)连接DE,求证:四边形CBED是平行四边形.
分析 (1)由SSS证明△ADC≌△CEB即可;
(2)由全等三角形的性质得出得到∠ACD=∠CBE,证出CD∥BE,即可得出结论.
解答  (1)证明:∵点C是AB的中点,
(1)证明:∵点C是AB的中点,
∴AC=BC;在△ADC与△CEB中,$\left\{\begin{array}{l}{AD=CE}&{\;}\\{CD=BE}&{\;}\\{AC=BC}&{\;}\end{array}\right.$,
∴△ADC≌△CEB(SSS),
(2)证明:连接DE,如图所示:
∵△ADC≌△CEB,
∴∠ACD=∠CBE,
∴CD∥BE,
又∵CD=BE,
∴四边形CBED是平行四边形.
点评 该题主要考查了平行四边形的判定、平行线的判定、全等三角形的判定与性质;熟练掌握平行四边形的判定,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
5.一艘轮船在静水中的最大航速为35km/h,它以最大航速沿江顺流航行120km所用时间,与以最大航速逆流航行90km所用时间相等.设江水的流速为v km/h,则可列方程为( )
| A. | $\frac{120}{v+35}$=$\frac{90}{v-35}$ | B. | $\frac{120}{35-v}$=$\frac{90}{35+v}$ | C. | $\frac{120}{v-35}$=$\frac{90}{v+35}$ | D. | $\frac{120}{35+v}$=$\frac{90}{35-v}$ |
3. 某几何体的三视图如图所示,则该几何体是( )
某几何体的三视图如图所示,则该几何体是( )
 某几何体的三视图如图所示,则该几何体是( )
某几何体的三视图如图所示,则该几何体是( )| A. | 球 | B. | 圆柱 | C. | 三棱锥 | D. | 圆锥 |
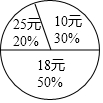 某餐厅供应单价为10元、18元、25元三种价格的抓饭,如图是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图可算得该餐厅销售抓饭的平均单价为17元.
某餐厅供应单价为10元、18元、25元三种价格的抓饭,如图是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图可算得该餐厅销售抓饭的平均单价为17元.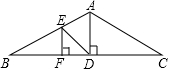 如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.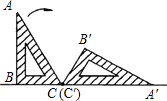 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为16πcm.
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为16πcm. 如图,AB∥CD,∠1=60°,则∠2=120°.
如图,AB∥CD,∠1=60°,则∠2=120°.