题目内容
8.已知关于x的方程x2+ax+a-2=0.(1)若该方程的一个根为2,求a的值及该方程的另一根.
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
分析 (1)解:设方程的另一根为t,利用根与系数的关系得到2+t=-a,2t=a-2,然后通过解方程组可得到a和t的值;
(2)先计算判别式的值得到△=a2-4(a-2)=(a-2)2+4,然后利用非负数的性质得到△>0,则根据判别式的意义可判断不论a取何实数,该方程都有两个不相等的实数根.
解答 (1)解:设方程的另一根为t,
根据题意得2+t=-a,2t=a-2,
所以2+t+2t=-2,解得t=-$\frac{4}{3}$,
所以a=-$\frac{2}{3}$;
(2)证明:△=a2-4(a-2)
=a2-4a+8
=(a-2)2+4,
∴△>0,
∴不论a取何实数,该方程都有两个不相等的实数根.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
18.把抛物线y=-x2向右平移1个单位,然后向下平移3个单位,则平移后抛物线的解析式为( )
| A. | y=-(x-1)2-3 | B. | y=-(x+1)2-3 | C. | y=-(x-1)2+3 | D. | y=-(x+a)2+3 |
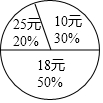 某餐厅供应单价为10元、18元、25元三种价格的抓饭,如图是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图可算得该餐厅销售抓饭的平均单价为17元.
某餐厅供应单价为10元、18元、25元三种价格的抓饭,如图是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图可算得该餐厅销售抓饭的平均单价为17元.
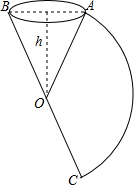 如图,将扇形AOC围成一个圆锥的侧面.已知围成的圆锥的高为12,扇形AOC的弧长为10π,则圆锥的侧面积为65π.
如图,将扇形AOC围成一个圆锥的侧面.已知围成的圆锥的高为12,扇形AOC的弧长为10π,则圆锥的侧面积为65π. 如图,AB∥CD,∠1=60°,则∠2=120°.
如图,AB∥CD,∠1=60°,则∠2=120°. 如图所示,AB∥CD,EC⊥CD.若∠BEC=30°,则∠ABE的度数为120°.
如图所示,AB∥CD,EC⊥CD.若∠BEC=30°,则∠ABE的度数为120°.