题目内容
2.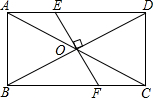 如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2$\sqrt{3}$,∠AEO=120°,则FC的长度为( )
如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2$\sqrt{3}$,∠AEO=120°,则FC的长度为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 先根据矩形的性质,推理得到OF=CF,再根据Rt△BOF求得OF的长,即可得到CF的长.
解答 解: ∵EF⊥BD,∠AEO=120°,
∵EF⊥BD,∠AEO=120°,
∴∠EDO=30°,∠DEO=60°,
∵四边形ABCD是矩形,
∴∠OBF=∠OCF=30°,∠BFO=60°,
∴∠FOC=60°-30°=30°,
∴OF=CF,
又∵Rt△BOF中,BO=$\frac{1}{2}$BD=$\frac{1}{2}$AC=$\sqrt{3}$,
∴OF=tan30°×BO=1,
∴CF=1,
故选:A.
点评 本题主要考查了矩形的性质以及解直角三角形的运用,解决问题的关键是掌握:矩形的对角线相等且互相平分.

练习册系列答案
相关题目
 如图,AB∥CD,∠1=60°,则∠2=120°.
如图,AB∥CD,∠1=60°,则∠2=120°.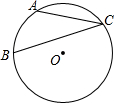 如图,点A、B、C在半径为1的⊙O上,$\widehat{AB}$的长为$\frac{2}{5}$π,则∠ACB的大小是36°.
如图,点A、B、C在半径为1的⊙O上,$\widehat{AB}$的长为$\frac{2}{5}$π,则∠ACB的大小是36°.