Question

1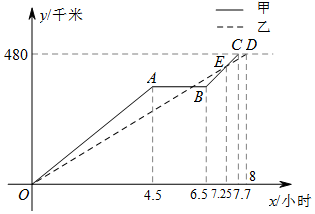．重阳节期间，某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游，由于人数较多，共租用甲、乙两辆长途汽车沿同一路线赶赴景点．图中的折线、线段分别表示甲、乙两车所走的路程y_甲（千米），y_乙（千米）与时间x（小时）之间的函数关系对应的图象．请根据图象所提供的信息，解决下列问题：
（1）由于汽车发生故障，甲车在途中停留了2小时；
（2）甲车排除故障后，立即提速赶往景点．请问甲车在排除故障时，距出发点的路程是多少千米？
（3）为了保证及时联络，甲、乙车在第一次相遇时约定此后两车之间的路程不超过35千米，请通过计算说明，按图象所表示的走法是否符合约定．

Answer 1

分析 （1）观察图象，利用修好车的时间-车刚坏的时间即可得出结论；
（2）由待定系数法先求出直线OD的解析式，求出点E坐标、点C的坐标，再求出直线BC的解析式，求出点B坐标即可；
（3）结合函数图象可知在B、D两点处甲、乙两个家庭距离最远，结合（2）得出的两函数解析式即可求出在B、C点时两个家庭之间的距离，再于25千米进行比较即可得出结论；

解答 解：（1）观察图象可知，甲车在途中停留了6.6-4.5=2小时，
故答案为2．

（2）由题意直线OD的解析式为y=60x，设直线BC的解析式为y=kx+b，
∵E（7.25，435），C（7.7，480），
则有$\left\{\begin{array}{l}{7.25k+b=435}\\{7.7k+b=480}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=100}\\{b=-290}\end{array}\right.$，
∴y=100x-290，
x=6.5时，y=360，
∴甲车在排除故障时，距出发点的路程是360千米

（3）符合约定．
由图象可知：甲乙两个家庭第一次相遇后在B和C相距最远．
在点B处有y_乙-y_甲=60×6.5-360=30千米＜35千米；
在点C处有y_甲-y_乙=100×7.7-290-（60×7.7）=18千米＜35千米．
∴按图象所表示的走法符合约定．

点评 本题考查了一次函数的应用以及待定系数法求函数解析式，解题的关键是：（1）结合函数图象解决问题；（2）利用待定系数法求出函数解析式；（3）求出在B、C两点处两家庭之间的距离．本题属于中档题，难度不大，但较繁琐，解决该类题型时，根据函数图象找出点的坐标，再利用待定系数法求出函数解析式是关键．