题目内容
14．若$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2），且（k$\overrightarrow{a}$+$\overrightarrow{b}$）∥（$\overrightarrow{a}$-3$\overrightarrow{b}$），则实数k的值是-$\frac{1}{3}$．分析 由$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2），可求得k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-3$\overrightarrow{b}$，然后由平行向量的性质，求得答案．
解答 解：∵$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2），
∴k$\overrightarrow{a}$+$\overrightarrow{b}$=（k-3，2k+2），$\overrightarrow{a}$-3$\overrightarrow{b}$=（10，-4），
∵（k$\overrightarrow{a}$+$\overrightarrow{b}$）∥（$\overrightarrow{a}$-3$\overrightarrow{b}$），
∴-4（k-3）-10（2k+2）=0，
解得：k=-$\frac{1}{3}$．
故答案为：-$\frac{1}{3}$．
点评 此题考查了平行向量的知识．注意根据题意分别求得k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-3$\overrightarrow{b}$是关键．
练习册系列答案
相关题目
如图，一次函数y=ax+b与反比例函数y=$\frac{k}{x}$（x＜0）的图象交于点A．与x轴、y轴分别交于点B、C，过点A作AD⊥x轴于点D，过点D作DE∥AB，交y轴于点E．己知四边形ADEC的面积为6．
如图，在△ABC中，∠BAC=90°，AB=8，AC=6，O为BC的中点，OE平分∠AOB，与AB相交于点E，OD平分∠AOC，与AC相交于点D．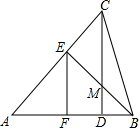
在△ABC中，CD是高，在边AC上有一点E，使EA=EB连接EB交CD于点M．