题目内容
19.若关于x的不等式组$\left\{\begin{array}{l}{5x+2a>0}\\{3a-x≥2}\end{array}\right.$的整数解是0,1,2,3,求a的取值范围.分析 先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其整数解,进而求得a的取值范围.
解答 解:$\left\{\begin{array}{l}{5x+2a>0①}\\{3a-x≥2②}\end{array}\right.$
由①得x>-$\frac{2a}{5}$,
由②得x≤3a-2,
∴不等式组的解集为-$\frac{2a}{5}$<x≤3a-2,
∵-$\frac{2a}{5}$<x≤3a-2的整数解是0,1,2,3,
∴-$\frac{2a}{5}$<0,3≤3a-2<4
∴$\frac{5}{3}$<a<2
∴a的取值范围是$\frac{5}{3}$<a<2.
点评 本题考查一元二次不等式的解法,考查学生分析解决问题的能力,属中档题.

练习册系列答案
相关题目
11.下列各组方程中,属于二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{2}=1}\\{3x+6y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x+2y=7}\\{xy=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+y=1}\\{x+z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{5}{x}+\frac{y}{3}=\frac{1}{2}}\\{x+2y=3}\end{array}\right.$ |
15.下列事件是不确定事件的是( )
| A. | 抛出的石块会下落 | |
| B. | 当室外温度低于-3℃时,将一碗清水放到室外,水会结冰 | |
| C. | 任意买一张电影票,座位号是奇数 | |
| D. | 地球绕着太阳转 |
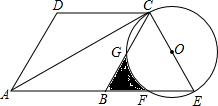 如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.
如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.