题目内容
4. 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.(1)求k的值;
(2)若AD=3OC,tan∠DAC=2.求点E的坐标.
分析 (1)设A(x,y),则AD=y,OD=-x,再由AD⊥x轴,DE∥AB得出四边形ADEC是平行四边形,故可得出AD•OD=6,由此可得出结论;
(2)根据AD=3OC,tan∠DAC=2,可设OC=x,则AD=3x,OD=6x,代入反比例函数的解析式得出x的值,由平行四边形的性质即可得出结论.
解答 解:(1)设A(x,y),则AD=y,OD=-x,
∵AD⊥x轴,DE∥AB,CE⊥x轴,
∴四边形ADEC是平行四边形.
∵四边形ADEC的面积为6,
∴AD•OD=6,即-xy=6,
∴k=xy=-6;
(2)∵AD=3OC,tan∠DAC=2,
∴设OC=x,则AD=3x,OD=6x,
∴A(-6x,3x),
∵点A在反比例函数y=-$\frac{6}{x}$的图象上,
∴-18x2=-6,解得x=$\frac{\sqrt{3}}{3}$,
∴OC=$\frac{\sqrt{3}}{3}$,AD=$\sqrt{3}$,
∵四边形ADEC是平行四边形,
∴AD=CE,
∴OE=CE-OC=$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
∴E(0,-$\frac{2\sqrt{3}}{3}$).
点评 本题考查的是反比例函数与一次函数的交点问题,根据题意判断出四边形ADEC是平行四边形是解答此题的关键.

练习册系列答案
相关题目
13.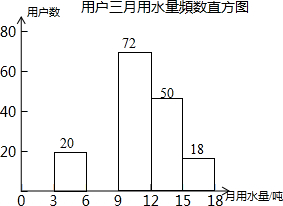 每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=40,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费.请估计该社区约有多少户家庭三月份的用水量超过基本月用水量?
 每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用水量h(吨) | 频数 | 频率 |
| h≤3 | 0 | 0 |
| 3<h≤6 | 20 | 0.10 |
| 6<h≤9 | m | 0.20 |
| 9<h≤12 | 72 | 0.36 |
| 12<h≤15 | 50 | n |
| 15<h≤18 | 18 | 0.09 |
| 18<h | 0 | 0 |
(1)在频数分布表中:m=40,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费.请估计该社区约有多少户家庭三月份的用水量超过基本月用水量?
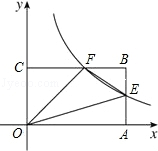 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则:
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则: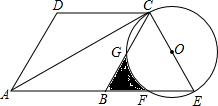 如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.
如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.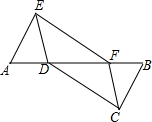 如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.
如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.