题目内容
6.根据不等式的基本性质,把下列各式化成“x>a”或“x<a”的形式.(1)x-2<3x-3;
(2)-x+2<x-6;
(3)3x+3<0;
(4)-2x+1<x+4.
分析 (1)根据不等式的性质1和不等式的性质3可以解答本题;
(2)根据不等式的性质1和不等式的性质3可以解答本题;
(3)根据不等式的性质1和不等式的性质2可以解答本题;
(4)根据不等式的性质1和不等式的性质3可以解答本题.
解答 解:(1)x-2<3x-3
两边同时加上2,得
x<3x-1
两边同时减去3x,得
-2x<-1
两边同时除以-2,得
x>$\frac{1}{2}$;
(2)-x+2<x-6
两边同时减去2,得
-x<x-8
两边同时减去x,得
-2x<-8
两边同时除以-2,得
x>4;
(3)3x+3<0
两边同时减去3,得
3x<-3
两边同时除以3,得
x<-1;
(4)-2x+1<x+4
两边同时减去1,得
-2x<x+3
两边同时减去x,得
-3x<3
两边同时除以-3,得
x>-1.
点评 本题考查不等式的性质,解题的关键是明确不等式的性质,尤其是要注意不等式的性质3,不等式两边同时乘以或除以同一个负数,不等式的符号要改变.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
11.下列各组方程中,属于二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{2}=1}\\{3x+6y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x+2y=7}\\{xy=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+y=1}\\{x+z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{5}{x}+\frac{y}{3}=\frac{1}{2}}\\{x+2y=3}\end{array}\right.$ |
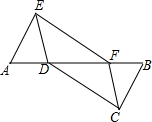 如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.
如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.