Question

14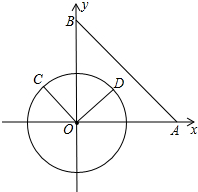．在平面直角坐标系xOy中，已知点A（8，0），点B（0，8），动点在以半径为4的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．
（1）当OC∥AB时，∠BOC的度数为45°；
（2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值．
（3）连接AD，当OC∥AD时，
①求出点C的坐标；
②直线BC是否为⊙O的切线？请作出判断，并说明理由．

Answer 1

分析 （1）由A与B的坐标可知：∠OBA=45°，当OC∥AB时，∠BOC=∠ABO=45°；
（2）过点C作CE⊥AB于点E，当E为AB中点时，△ABC的面积有最大值，此时只需要求出CE的值即可求出△ABC的面积；
（3）①当OC∥AD时，此时∠ODA=90°，即点D在以OA为直径的圆上，作出以AB为直径的⊙F，⊙F与⊙O相交于点D₁，D₂，又因为OC⊥OD，所以可求出分别求出点C的坐标；
②连接BC后，求出OG，BG的长度，然后求出tan∠CBG的值，即可求得∠CBG=30°，所以∠OCB=90°．

解答 （1）∵A（8，0），B（0，8），
∴OA=OB=8，
当OC∥AB时，
∴∠BOC=∠ABO=45°；

（2）如图1，过点C作CE⊥AB于点E，
当E为AB中点时，△ABC的面积有最大值，
由勾股定理可求得：AB=8$\sqrt{2}$，
∴OE=4$\sqrt{2}$，
又∵OC=4，
∴CE=OC+OE=4+4$\sqrt{2}$，
∴△ABC的面积为：$\frac{1}{2}$AB•CE=$\frac{1}{2}$×$8\sqrt{2}$×（4+4$\sqrt{2}$）=16$\sqrt{2}$+32；

（3）当OC∥AD时，
∴∠ODA=90°，
∴由圆周角定理可知：D在以OA为直径的圆上，
如图2，以OA为直径作⊙F，交⊙O于点D₁，D₂，
①连接D₁F，
∴D₁F=$\frac{1}{2}$OA，
∴△OD₁F是等边三角形，
∴∠D₁OA=60°，
∵∠C₁OD₁=90°，
∴∠C₁OB=60°，
过点C₁作C₁G⊥y轴，
∴OG=2，
由勾股定理可知：C₁G=2$\sqrt{3}$，
∴C₁（-2$\sqrt{3}$，2），
同理可知：∠D₂OA=60°，
∴∠C₂OA=30°，
∴∠C₂OB=60°
由圆的对称性可知：C₁与C₂关于y轴对称，
∴C₂（2$\sqrt{3}$，2），
综上所述，当OC∥AD时，点C的坐标为（-2$\sqrt{3}$，2）或（2$\sqrt{3}$，2）；

②如图3，连接BC₁，
由①可知：OG=2，C₁G=2$\sqrt{3}$，
∴BG=OB-OG=8-2=6，
∴tan∠C₁BG=$\frac{{C}_{1}G}{BG}$=$\frac{\sqrt{3}}{3}$，
∴∠C₁BG=30°，
又∵∠C₁OB=60°，
∴∠BC₁O=90°，
∴BC₁与⊙O相切，
∴由圆的对称性可知：BC₂与⊙O相切，
综上所述，当OC∥AD时，BC与⊙O相切．

点评 本题考查圆的综合问题，涉及锐角三角函数，圆周角定理，圆的切线判定，等边三角形的性质等知识内容，本题综合程度较高，需要学生综合运用所学知识解决．