题目内容
2.我们称顶点相同的两条抛物线为同位抛物线,已知抛物线C1:y=2x2-4x+3.(1)下列抛物线中,与C1是同位抛物线的是B.
A.y=2x2-4x+4 B.y=3x2-6x+4
C.y=-2x2-4x+3 D.y=2x2
(2)若抛物线C2:y=ax2-2ax+c(a≠0)与C1是同位抛物线,则a与c需满足什么关系?
分析 (1)求各函数的顶点坐标,根据顶点相同的两条抛物线为同位抛物线,做判断;
(2)先表示抛物线C2的顶点坐标,再列式计算.
解答 解:抛物线C1:y=2x2-4x+3.
y=2(x2-2x+1-1)+3
y=2(x-1)2+1,顶点为(1,1)
A、y=2x2-4x+4=2(x-1)2+2,顶点为(1,2),所以A不正确;
B、y=3x2-6x+4=3(x-1)2+1,顶点为(1,1),所以B正确;
C、y=-2x2-4x+3=-2(x+1)2+5,顶点为(-1,5),所以C不正确;
D、y=2x2,顶点为(0,0),所以D不正确;
故选B.
(2)抛物线C2:y=ax2-2ax+c
y=a(x2-2x+1-1)+c
y=a(x-1)2-a+c,顶点为(1,-a+c)
由抛物线C2:y=ax2-2ax+c(a≠0)与C1是同位抛物线得:-a+c=1,c-a=1
∴a与c需满足的关系式为:c-a=1
点评 本题考查了同位抛物线的判定,正确求二次函数的顶点坐标是本题的关键;可利用两种方法求顶点坐标:①利用配方法求解,形如y=a(x-h)2+k的顶点坐标为(h,k);②利用顶点坐标公式(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)求解.

练习册系列答案
相关题目
8. 五个大小相同的正方体搭成的几何体如图所示,其主视图是( )
五个大小相同的正方体搭成的几何体如图所示,其主视图是( )
 五个大小相同的正方体搭成的几何体如图所示,其主视图是( )
五个大小相同的正方体搭成的几何体如图所示,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
13.计算(a4b)2÷a2的结果是( )
| A. | a2 b2 | B. | a6 b2 | C. | a7 b2 | D. | a8 b2 |
17.分式方程$\frac{2x+1}{3-x}$=1的解是( )
| A. | x=-$\frac{1}{2}$ | B. | x=2 | C. | x=3 | D. | x=$\frac{2}{3}$ |
12.下列计算正确的是( )
| A. | -3÷3×3=-3 | B. | -3-3=0 | C. | -3-(-3)=-6 | D. | -3÷3÷3=-3 |
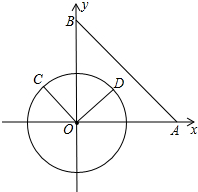 在平面直角坐标系xOy中,已知点A(8,0),点B(0,8),动点在以半径为4的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
在平面直角坐标系xOy中,已知点A(8,0),点B(0,8),动点在以半径为4的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.